- 两圆的公切线条数及方程的确定
- 共94题
如图,












正确答案

解析
略
知识点
若直线


正确答案
解析
略
知识点
定义









(1)比较

(2)设函数






(3)设数列













正确答案
见解析
解析
(1)设数列



所以
当




所以

所以


(2)假设存在实数



即

由(1)知数列


解得

所以存在最大的实数



(3)由


① 若










此时,






② 若





所以




设数列




即


知识点
已知椭圆G:


(1)求椭圆G的方程;
(2)在直线l的斜率k变化的过程中,是
个常数

这个常数
正确答案
见解析
解析
(1)解:设





(2)存在常数
解法一:设

于是 
直线AM的斜率

则


同理可得

同理可得

综上可知,存在常数
解法二:设

于是 
A、B关于x轴的对称点分别为



所以







知识点
已知









(1)求

(2 )证明:
(3)设点

正确答案
见解析。
解析
解:(1)由已知得






(2)
当
又当

(3)假设存在两点





设





知识点
在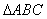

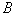
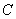
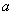
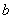
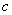
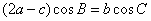
(1)求角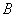
(2)若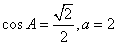
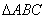
正确答案
(1)
(2)
解析
(1)因为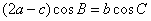

∴ 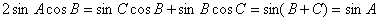
∵ 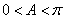
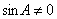
∴ 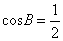
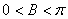
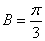
(2)由正弦定理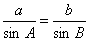
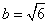
由 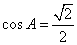
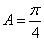
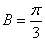
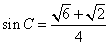
∴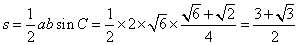
知识点
已知直线


(1)写出直线
(2)设




正确答案
见解析。
解析
(1)直线的参数方程为

(2)把直线






知识点
求曲线2x2﹣2xy+1=0在矩阵MN对应的变换作用下得到的曲线方程,其中

正确答案
见解析。
解析
∵

∴MN=

设P(x′,y′)是曲线2x2﹣2xy+1=0上任意一点,点P在矩阵MN对应的变换下变为点P′(x,y),
则有

于是x′=x,y′=x+
代入2x′2﹣2x′y′+1=0得xy=1,
所以曲线2x2﹣2xy+1=0在MN对应的变换作用下
得到的曲线方程为xy=1.
所以曲线2x2﹣2xy+1=0在MN对应的变换作用下得到的曲线方程为xy=1
知识点
已知函数


正确答案
解析

由

知识点
如图,对大于等于2的自然数


正确答案
11;
解析
对大于或等于2的自然数m的n次幂进行如下方式的“分裂”,不难发现:在n2中所分解的最大的数是2n-1;故62的“分裂”中最大的数是11;在m3(m为奇数)的“分拆”的最大数是m2+m-1,所以20132+2012=4054181,写成“20132+2012”或“4054181”故答案为:11;20132+2012。
知识点
扫码查看完整答案与解析