两圆的公切线条数及方程的确定
共94题

· 两圆的公切线条数及方程的确定

两圆的公切线条数及方程的确定
共94题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

9.在中,角A,B,C的对边分别是,且则等于( )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：简答题

简答题 · 10 分

请在第22、23、24三题中任选一题作答，如果多做，则按所做第一题记分。

22.选修4-1：几何证明选讲

如图，D，E分别为的边AB，AC上的点，且不与的顶点重合．已知AE的长为m，AC的长为n，AD，AB的长是关于x的方程的两个根．

（I）证明：C，B，D，E四点共圆；

（II）若，且求C，B，D，E所在圆的半径．

23．选修4-4：坐标系与参数方程

在直角坐标系xOy中，曲线的参数方程为为参数），M为上的动点，P点满足，点P的轨迹为曲线．

（I）求的方程；

（II）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线与的异于极点的交点为A，与的异于极点的交点为B，求|AB|.

24．已知，且，求的最小值及取得最小值时的值

正确答案

22.

23.

24.

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：填空题

填空题 · 5 分

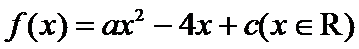
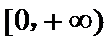
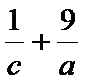
14．已知二次函数的值域为，则的最小值为_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：简答题

简答题 · 12 分

21．已知函数，其中．

（Ⅰ）若是的极值点，求的值；

（Ⅱ）求的单调区间；

（Ⅲ）若在上的最大值是，求的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：单选题

单选题 · 5 分

12．是定义在区间【-c，c】上的奇函数，其图象如图所示,令，则下列关于函数的叙述正确的是（）

A若，则函数的图象关于原点对称

B若，，则方程必有三个实根

C若，，则方程必有两个实根

D若，，则方程必有大于2的实根

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：简答题

简答题 · 12 分

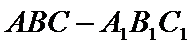
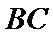
19．已知直三棱柱的三视图如图所示，且是的中点．

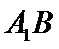
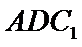
（Ⅰ）求证：∥平面；

（Ⅱ）求二面角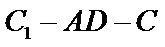的余弦值；

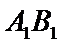
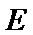
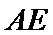
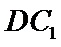
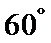
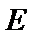
（Ⅲ）试问线段上是否存在点，使与成角？若存在，确定点位置，若不存在，说明理由．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：简答题

简答题 · 13 分

20．已知函数，

（1）若求的值域；

（2）若存在实数，当恒成立，求实数的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：单选题

单选题 · 5 分

15．“”是“”的（）

A充分非必要条件

B必要非充分条件

C充要条件

D既非充分又非必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：简答题

简答题 · 14 分

21．在平面直角坐标系中，已知点、，是动点，且直线与的斜率之积等于．

（1）求动点的轨迹方程；

（2）设直线与分别与直线相交于点、，试问：是否存在点使得与的面积相等？若存在，求出点的坐标；若不存在，说明理由．

正确答案

（1）设点的坐标为，由题意得

化简得．

故动点的轨迹方程为

（2）解法一：设点的坐标为，点，得坐标分别为,．

则直线的方程为，直线的方程为

令得，．

于是的面积

又直线的方程为，，

点到直线的距离．

于是的面积

当时，得

又，所以=，

解得，因为，所以

故存在点使得与的面积相等，此时点的坐标为．

解法二：若存在点使得与的面积相等，设点的坐标为

则．

因为,

所以

即，

解得，因为，所以

故存在点使得与的面积相等，此时点的坐标为

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

题型：单选题

单选题 · 5 分

10．已知的坐标满足：，那么的取值范围是（）

A[1,4]

B[1,5]

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两圆的公切线条数及方程的确定

继续学习学习下一知识点

下一知识点 : 圆系方程

百度题库 > 高考 > 理科数学 > 两圆的公切线条数及方程的确定

扫码查看完整答案与解析