- 抽象函数及其应用
- 共45题
2.已知c>b,且f(x)在两个区间[a,b],[c,d]上都是增函数,若补充条件使得f(x)在集合[a,b]∪[c,d]上也是增函数,则应补充的条件是( )
正确答案
解析
由题意,任取
①若x1,x2∈[a,b],由f(x)在[a,b]是增函数,
必有f(x1)<f(x2)成立;
②若x1,x2∈[c,d],由f(x)在[c,d]是增函数,
必有f(x1)<f(x2)成立;
③若a≤x1≤b<c≤x2≤d,
由题设知f(x1)<f(b)且f(c)≤f(x2),
又∵f(b)<f(c),
∴f(x1)<f(x2).
综上所述,f(x)在
知识点
12.已知函数f(x)是定义在R上的奇函数,并满足f(x-4)=-f(x)且在[0,2]上是增函数,给出下列结论:
(1)若0<x1<x2<4,且x1+x2=4,则f(x1)+f(x2)>0;
(2)若0<x1<x2<4,且x1+x2=5,则f(x1)>f(x2);
(3)若方程f(x)=m在[-8,8]内恰有四个不同的根x1,x2,x3,x4,则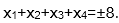
正确答案
解析
∵f(x-4)=-f(x),
∴f(x-8)=-f(x-4)=f(x),
∴f(x)的周期为8.
∵函数f(x)是定义在R上的奇函数,
∴f(x)关于原点对称.
∵f(x-4)=-f(x),∴f(x-4)=f(-x),
∴f(x)关于x=-2对称.
由f(x)关于原点对称,
∴f(x)也关于x=2对称.
由f(x)在[0,2]上是增函数,且f(0)=f(4)=0,则可以画出草图为
(1)若0<x1<x2<4,且x1+x2=4,则可得到x1,x2关于x=2对称,
由图可知f(x1)>0,f(x2)>0,
所以f(x1)+f(x2)>0,故(1)正确.
(2)若0<x1<x2<4,且x1+x2=5,则可得x2到x=2的距离比x1到x=2的距离要远,
由图象可得f(x1)>f(x2),故(2)正确.
(3)如图所示,若m>0,则两个根关于x=-6对称,两个根关于x=2对称,
所以有x1+x2+x3+x4=-8.若m<0,
则两个根关于x=-2对称,
两个根关于x=6对称,所以有x1+x2+x3+x4=8,
故(3)也正确.
本题答案为D.
知识点
4.f (x)是定义在R上的奇函数,对任意


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数f(x)的定义域为[3,6],则函数y=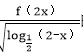
正确答案
解析
∵f(x)的定义域为[3,6],∴函数f(2x)中2x∈[3,6],∴
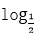

知识点
8.若f(x)是奇函数,且在(-∞,0)上是增函数,又f(-2)=0,则满足xf(x-1)>0的x取值范围为_________.
正确答案
解析
画一个草图,
由xf(x-1)>0⇒
或
即x的取值范围为{x|x<-1或0<x<1或x>3}.
知识点
扫码查看完整答案与解析









