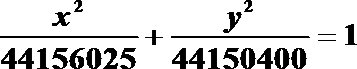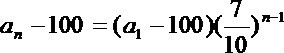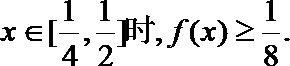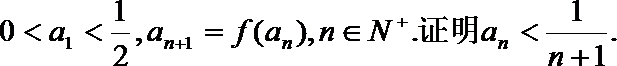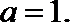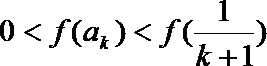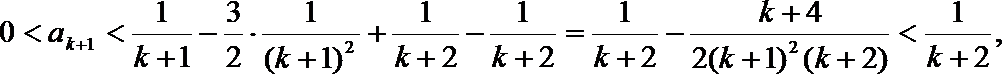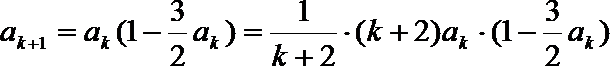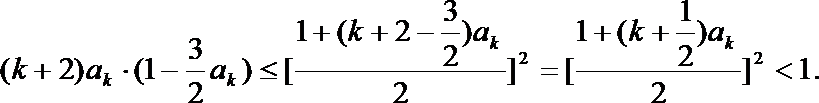2.已知直线l⊥平面α,直线m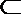
①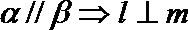
②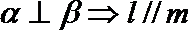
③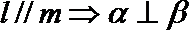
④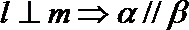
其中正确的两个命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
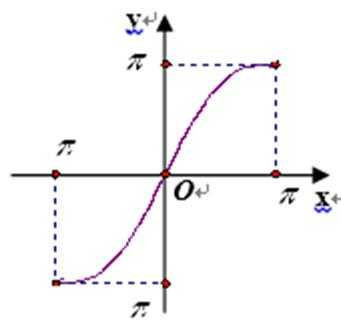
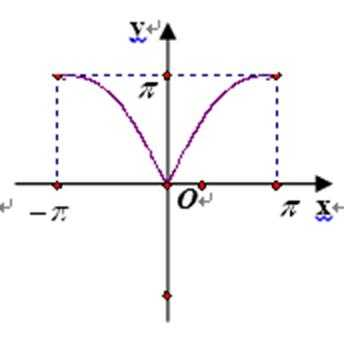
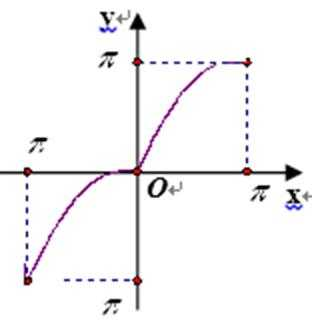
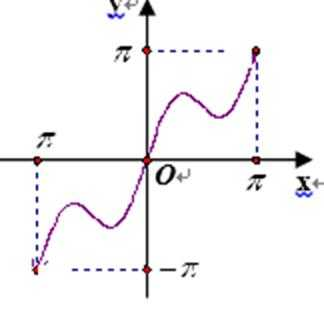
3.下列函数的图象中,经过平移或翻折后不能与函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.如右图所示,在正方体ABCD—A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 函数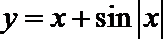
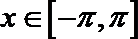
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设a、b是方程

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.等差数列{an}的前n项和为Sn,且a1>0,若存在自然数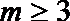
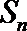
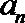
正确答案
<
解析
解析已在路上飞奔,马上就到!
知识点
9.若实数x、y满足
正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
14.某纺织厂的一个车间有n(n>7,n∈N)台织布机,编号分别为1,2,3,……,n,该车间有技术工人n名,编号分别为1,2,3,……,n.现定义记号




正确答案
1;第3名工人操作了两台织布机
解析
解析已在路上飞奔,马上就到!
知识点
11.2003年10月15日,我国自行研制的首个载人宇宙飞船“神州五号”在酒泉卫星发射中心胜利升空,实现了中华民族千年的飞天梦,飞船进入的是椭圆轨道,已知该椭圆轨道与地球表面的最近距离约为200公里,最远距离约350公里(地球半径约为6370公里),则轨道椭圆的标准方程为(精确到公里)______________.(注:地球球心位于椭圆轨道的一个焦点,写出一个方程即可)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.某民航站共有1到4四个入口,每个入口处每次只能进一个人,一小组4个人进站的方案数为______________.
正确答案
840
解析
解析已在路上飞奔,马上就到!
知识点
13.设
(1)


(2)



(3)
(4)若



(5)


(6)
其中真命题的序号为_____________________________.
正确答案
(3),(6)
解析
解析已在路上飞奔,马上就到!
知识点
17.某校有教职员工150人,为了丰富教工的课余生活,每天下午4:00~5:00同时开放健身房和娱乐室,要求所有教工每天必须参加一个活动.据调查统计,每次去健身房的人有10%下次去娱乐室,而在娱乐室的人有20%下次去健身房.请问,随着时间的推移,去健身房的人数能否趋于稳定?
正确答案
设第n次去健身房的人数为an,去娱乐室的人数为bn,则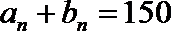
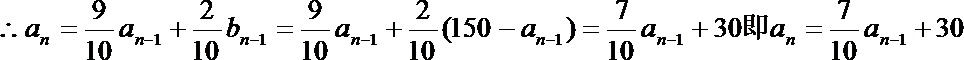
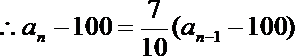
即 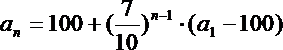
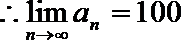
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数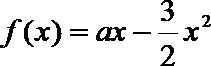

(1)求a的值;
(2)设
正确答案
(1)解:由于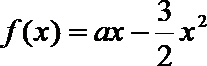
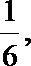
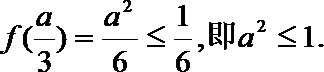
又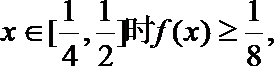
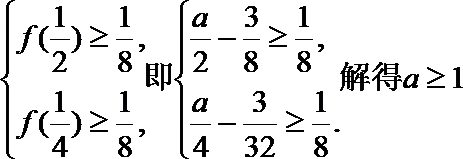
由①②得
(2)证法一:(i)当n=1时,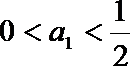
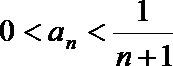
因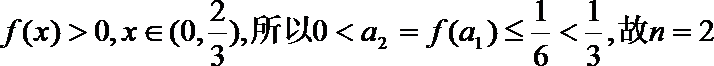
(ii)假设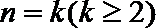
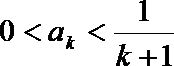
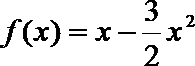
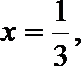
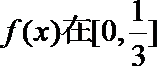
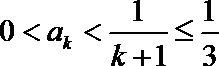
于是有
所以当n=k+1时,不等式也成立.
根据(i)(ii)可知,对任何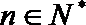
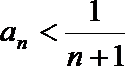
证法二:(i)当n=1时,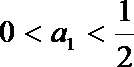
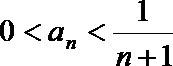
(ii)假设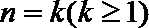
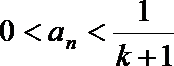
因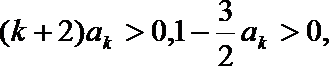
于是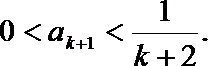
根据(i)(ii)可知,对任何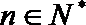
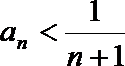
证法三:(i)当n=1时,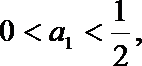
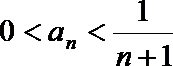
(ii)假设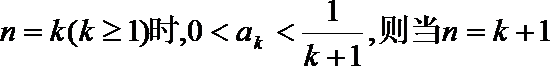
若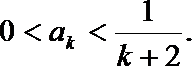
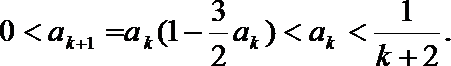
若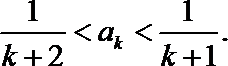
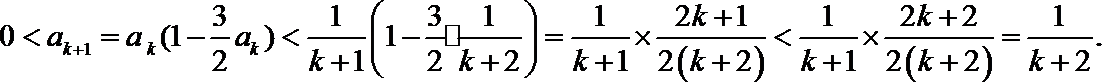
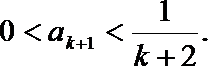
根据(i)(ii)可知,对任何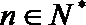
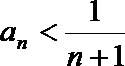
解析
解析已在路上飞奔,马上就到!
知识点
15.在ΔABC中,角A、B、C所对的边分别为

(1)求
(2)若
正确答案
(1)
=

(2) ∵
∴
又∵
∴
当且仅当 b=c=


解析
解析已在路上飞奔,马上就到!
知识点
16.如图,在棱长为1的正方体ABCD—A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.
(1)试确定点F的位置,使得D1E⊥平面AB1F;
(2)当D1E⊥平面AB1F时,求二面角C1—EF—A的大小(结果用反三角函数值表示).
正确答案
解法一:(1)连结A1B,则A1B是D1E在面ABB1A;内的射影。

∵AB1⊥A1B,∴D1E⊥AB1,
于是D1E⊥平面AB1F
连结DE,则DE是D1E在底面ABCD内的射影.
∴D1E⊥AF
∵ABCD是正方形,E是BC的中点.
∴当且仅当F是CD的中点时,DE⊥AF,
即当点F是CD的中点时,D1E⊥平面AB1F.
(2)当D1E⊥平面AB1F时,由(1)知点F是CD的中点.
又已知点E是BC的中点,连结EF,则EF∥BD. 连结AC,
设AC与EF交于点H,则CH⊥EF,连结C1H,则CH是C1H在底面ABCD内的射影.
C1H⊥EF,即∠C1HC是二面角C1—EF—C的平面角.
在Rt△C1CH中,∵C1C=1,CH=


又因为∠AHC1=

解法二:以A为坐标原点,建立如图所示的空间直角坐标系。
(1)设DF=x,则A(0,0,0),B(1,0,0),D(0,1,0),
A1(0,0,1),B(1,0,1),D1(0,1,1),E
∴
于是,
即

(2)当D1E⊥平面AB1F时,F是CD的中点,又E是BC的中点,连结EF,则EF∥BD. 连结AC,设AC与EF交于点H,则AH⊥EF. 连结C1H,则CH是C1H在底面ABCD内的射影.
∴C1H⊥EF,即∠AHC1是二面角C1—EF—A的平面角.


解析
解析已在路上飞奔,马上就到!
知识点
18.某人居住在城镇的A处,准备开车到单位B处上班. 若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为

(1)请你为其选择一条由A到B的最短路线(即此人只选择从西向东和从南向北的路线),使得途中发生堵车事件的概率最小;
(2)若记路线A→C→F→B中遇到堵车次数为随机变量

正确答案
(1)记路段MN发生堵车事件为MN.
因为各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,所以路线A→C→D→B中遇到堵车的概率P1为
1-P(
=1-[1-P(AC)][1-P(CD)][1-P(DB)]
=1-
同理:路线A→C→F→B中遇到堵车的概率P2为1-P(
路线A→E→F→B中遇到堵车的概率P3为1-P(
显然要使得由A到B的路线途中发生堵车事件的概率最小.只可能在以上三条路线中选择.
因此选择路线A→C→F→B,可使得途中发生堵车事件的概率最小。
(2)路线A→C→F→B中遇到堵车次数
答:路线A→C→F→B中遇到堵车次数的数学期望为
解析
解析已在路上飞奔,马上就到!
知识点
20.已知抛物线





(1)求证:直线
(2)分别以


正确答案
(1)证明:由题可知





所以,




同理可得:

直线


显然,不论


(2)过









即
又因为公共弦必与两圆的连心线垂直,所以公共弦的斜率为
所以,公共弦所在直线的方程为
即
所以公共弦恒过原点。
根据平面几何的知识知道:公共弦中点就是公共弦与两圆连心线的交点,所以原点




又对于圆上任意一点


解析
解析已在路上飞奔,马上就到!