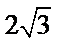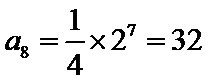3.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件.为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取 ▲ 件.
正确答案
18
解析
应从丙种型号的产品中抽取
考查方向
解题思路
根据分层抽样的特点,求解答案
易错点
相关概念掌握混淆
7.记函数




正确答案
解析
由


考查方向
解题思路
先求出函数的定义域,根据几何概型的计算公式计算
易错点
对几何概型的概念掌握混淆
8.在平面直角坐标系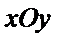
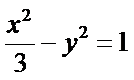
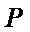
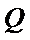
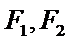
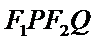
正确答案
解析
右准线方程为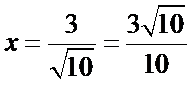
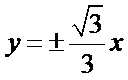
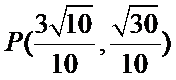
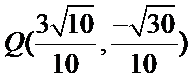
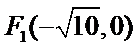
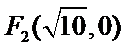
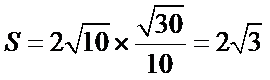
考查方向
解题思路
先求出右准线的方程,然后求出渐近线的方程,然后求解四边形的面积
易错点
计算能力弱
10.某公司一年购买某种货物600吨,每次购买


正确答案
30
解析
总费用为


考查方向
解题思路
根据实际问题的背景,整理化简成平均值不等式形式,然后利用不等式的性质求解答案
易错点
想不到利用平均值不等式求解答案
2.已知复数

正确答案
解析


考查方向
解题思路
按照服输的化简法则,逐步化简
易错点
计算错误
1.已知集合



正确答案
1
解析
由题意



考查方向
解题思路
先求出两个集合,然后根据集合的交集运算求解
易错点
求交集错误
4.右图是一个算法流程图,若输入


正确答案
解析
由题意得

考查方向
解题思路
根据所给数值判定是否满足判断框中的条件,然后执行循环语句,一旦满足条件就退出循环,输出结果.
易错点
循环结构的控制条件
5.若

正确答案
解析


考查方向
解题思路
根据同角的三角函数的性质,求解答案
易错点
相关性质定理掌握不牢固
6.如图,在圆柱






正确答案
解析
设球半径为


考查方向
解题思路
根据球和圆柱的关系,求解体积的比值
易错点
空间立体感不强
9.等比数列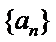
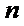
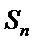
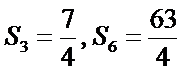
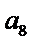
正确答案
32
解析
当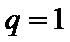
当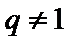
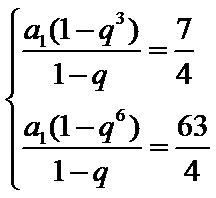
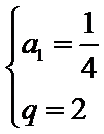
考查方向
解题思路
分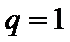
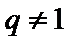
易错点
分情况讨论q的值
14.设






正确答案
8
解析
由于

在此范围内,



若



因此


因此

只需考虑

画出函数图象,图中交点除外

且


因此方程
考查方向
解题思路
根据周期函数的性质,结合函数图形,然后判断交点的个数
易错点
数形结合能力弱
11.已知函数


正确答案
解析
因为

因为


又



解得


考查方向
解题思路
根据函数的奇偶性和单调性判断函数的取值范围
易错点
计算化简过程中出现错误
12.如图,在同一个平面内,向量











正确答案
3
解析
由


易得



所以
考查方向
解题思路
根据向量的性质,分别求出角度的正弦值和余弦值,然后利用向量的分解方式求解答案
易错点
考虑不到利用向量的分解方法求解。
13.在平面直角坐标系





正确答案
解析
设






考查方向
解题思路
利用数形结合方法,根据题中所给的限制条件,求解P点横坐标的取值范围
易错点
数形结合能力差
15.(本小题满分14分)
如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
正确答案
详见解析
解析
(1)在平面ABD内,因为AB⊥AD,EF⊥AD,所以EF//AB
又因为EF

(2)因为平面ABD


所以BC⊥平面ABD
因为AD
又AB⊥AD,BC


AC
考查方向
解题思路
(1)由线线平行,推出线面平行,再推出线线平行,(2)由面面垂直推出线面垂直,再推出线线垂直
易错点
线面平行的判定定理;面面垂直推出线面垂直
16.(本小题满分14分)
已知向量
(1)若a∥b,求x的值;
(2)记


正确答案
详见解析
解析
(1)因为


若


于是
(2)
因为


于是,当


当



考查方向
解题思路
(1)根据向量平行,得到等量关系,进而求

易错点
相关性质定义掌握不牢固
17.(本小题满分14分)
如图,在平面直角坐标系












(1)求椭圆
(2)若直线




正确答案
详见解析
解析
(1)设椭圆的半焦距为c.
因为椭圆E的离心率为


解得


(2)由(1)知,

设


当



当



因为





从而直线

直线

由①②,解得

因为点



又

由


因此点P的坐标为
考查方向
解题思路
(1)设出方程,根据题目所提供的坐标关系,求出椭圆方程中的待定系数,得出椭圆方程
(2)利用椭圆的对称性,建立等量关系,根据方程的解求出P点的坐标
易错点
计算能力弱
18.(本小题满分16分)
如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10


(1)将



(2)将



正确答案
详见解析
解析
(1)由正棱柱的定义,




记玻璃棒的另一端落在

因为


记


则P1Q1⊥平面ABCD,故P1Q1=12,从而AP1=
答:玻璃棒l没入水中部分的长度为16cm.
(如果将“没入水中部分”理解为“水面以上部分”,则结果为24cm)

(2)如图,O,
由正棱台的定义,

同理,平面

记玻璃棒的另一端落在
过G作GK⊥E1G1,K为垂足,则GK =OO1=32.
因为EG = 14,E1G1= 62,
所以KG1=

设

因为

在


因为

于是
记EN与水面的交点为P2,过P2作P2Q2⊥EG,Q2为垂足,则P2Q2⊥平面EFGH,
故P2Q2=12,从而EP2=
答:玻璃棒l没入水中部分的长度为20cm.
(如果将“没入水中部分”理解为“水面以上部分”,则结果为20cm)
考查方向
解题思路
(1)根据正棱柱的性质,求出相关线段的长(2)利用正弦定理求相关线段的长
易错点
立体感不强;计算能力弱;相关性质概念混淆
20.(本小题满分16分)
已知函数


(1)求

(2)证明:
(3)若



正确答案
详见解析
解析
|(1)由
当

因为

所以

因为


当



当



列表如下:
故




(2)由(1)知,


当



因为




(3)由(1)知,


从而
=
记


因为



因为


因为



考查方向
易错点
求导函数时错误,判断单调性时有重漏
19.(本小题满分16分)
对于给定的正整数





(1)证明:等差数列

(2)若数列



正确答案
详见解析
解析
(1)因为


从而,当

所以
因此等差数列

(2)数列


当

当

由①知,

将③④代入②,得

所以

在①中,取


在①中,取


所以数列
考查方向
解题思路
(1)根据所给条件,判断其为等差数列(2)根据所给条件,化简求解,判断其为邓婵数列
易错点
对等差数列的性质掌握不牢固
21.附加题【选做题】本题包括



B.[选修4-2:矩阵与变换](本小题满分10分)
已知矩阵
(1)求
(2)若曲线



正确答案
详见解析
解析
(1)因为

(2)


则







考查方向
解题思路
(1)根据矩阵的乘法计算法则计算求得(2)利用矩阵AB变换的性质,得到变换后的曲线方程
易错点
对矩阵的运算掌握不好
21. 附加题【选做题】本题包括



D.[选修4-5:不等式选讲](本小题满分10分)
已知

正确答案
详见解析
解析
由柯西不等式可得
因为


考查方向
解题思路
由柯西不等式可得
因为


易错点
均值不等式的取等条件
23. 【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.(本小题满分10分)
已知一个口袋中有






(1)试求编号为2的抽屉内放的是黑球的概率
(2)随机变量



正确答案
详见解析
解析
(1)编号为2的抽屉内放的是黑球的概率

(2)随机变量X的概率分布为
随机变量X的期望为
所以

即
考查方向
解题思路
(1)根据事件发生的概率,计算求得;(2)列出随机事件发生的分布列,利用二项式定理求得
易错点
计算化简能力弱
21.附加题【选做题】本题包括



如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足.
求证:(1)
(2)
正确答案
详见解析
解析
(1)因为

因为

因为AP⊥PC,所以

(2)由(1)知,


考查方向
解题思路
(1)根据切线的性质及圆周角的性质证明结论;(2)先判定两个三角形相似,然后利用相似三角形对应边成比例求解答案
易错点
相关性质定理记忆混淆
21. 附加题【选做题】本题包括



在平面直角坐标系










正确答案
详见解析
解析
直线




从而点




因此当点





考查方向
解题思路
先化成普通方程,然后利用点到直线的距离公式,求出最小值
易错点
直角坐标与极坐标的相互转化
22【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.(本小题满分10分)
如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=

(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
正确答案
详见解析
解析
在平面ABCD内,过点A作AE
因为AA1


如图,以
因为AB=AD=2,AA1=

则
(1)
则
因此异面直线A1B与AC1所成角的余弦值为
(2)平面






不妨取




从而
设二面角B-A1D-A的大小为

因为


考查方向
解题思路
(1)建立空间直角坐标系,然后计算求出异面直线所成的角(2)建立空间直角坐标系,然后计算求出异面直线所成的角
易错点
计算能力弱