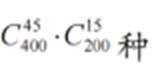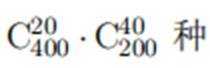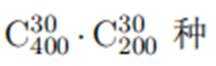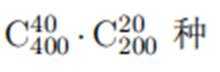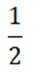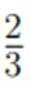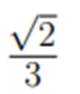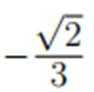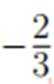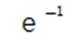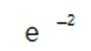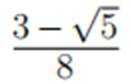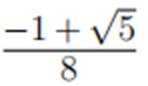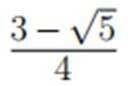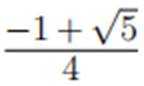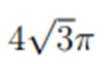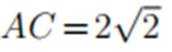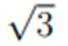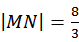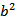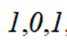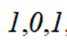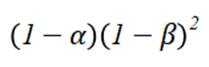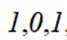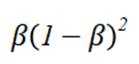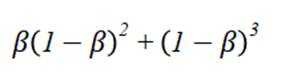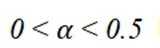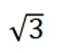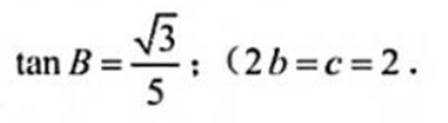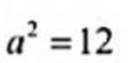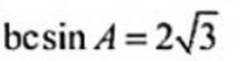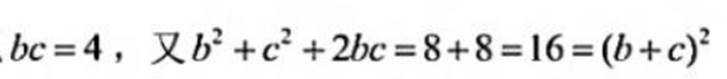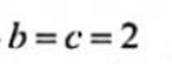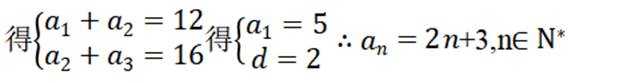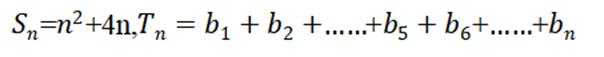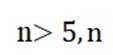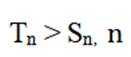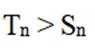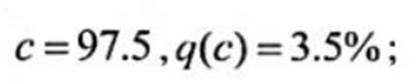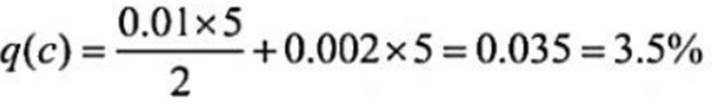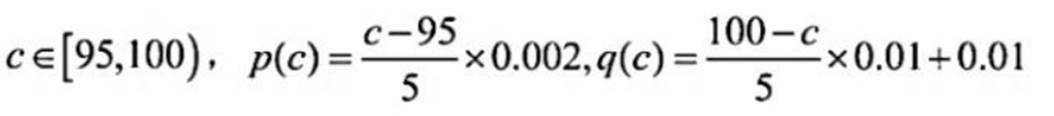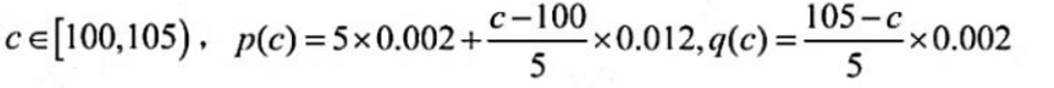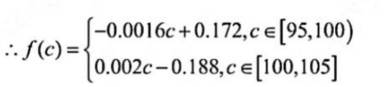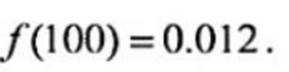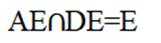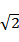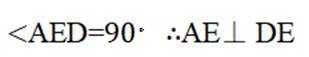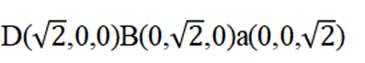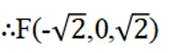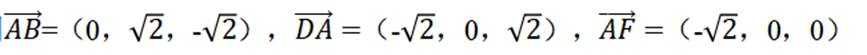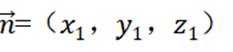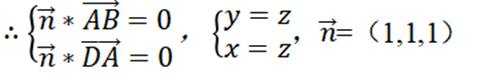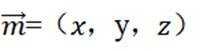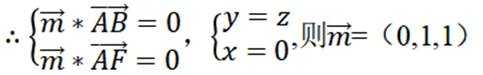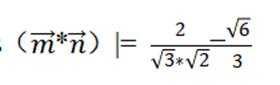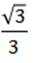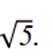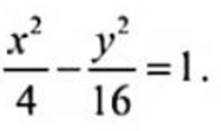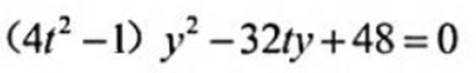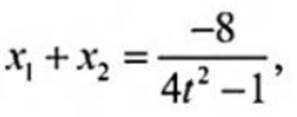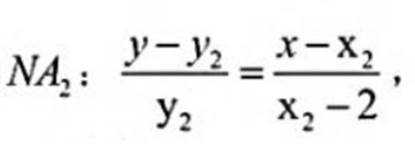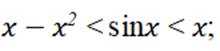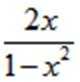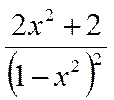在复平面内,(1+3i)(3−i)对应的点位于( )
正确答案
设集合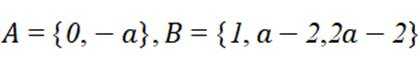
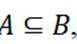
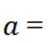
A2
B1
C
D−1
正确答案
某学校为了解学生参加体育运动的情况, 用比例分配的分层随机抽样方法作抽样调查,拟从初中部和高中部两层共抽取60名学生,已知该校初中部和高中部分别有400名和200名学生, 则不同的抽样结果共有 ( )
A
B
C
D
正确答案
若
A−1
B0
C
D1
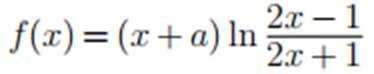
正确答案
已知椭圆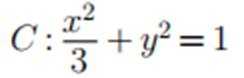
A
B
C
D
正确答案
已知函数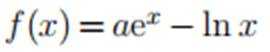 
Ae 2
Be
C
D
正确答案
已知 α 为锐角,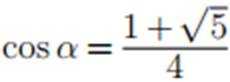 
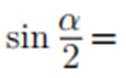
A
B
C
D
正确答案
记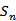
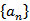
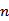
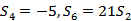
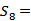
正确答案
已知圆锥的顶点为P,底面圆心为O,AB为底面直径,∠APB=120◦,PA=2,点C在底面圆周上,且二面角P−AC−O为45◦, 则 ( )
A该圆锥的体积为 π
B该圆锥的侧面积为
C
D△P AC 的面积为
正确答案
设O为坐标原点,直线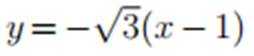
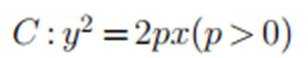
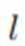
Ap = 2
B
C以 MN 为直径的圆与
D△OMN 为等腰三角形
正确答案
若函数
Abc > 0
Bab > 0
C
Dac < 0
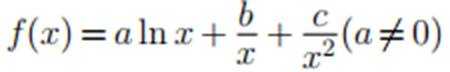
正确答案
在信道内传输 0,1 信号, 信号的传输相互独立, 发送 0 时, 收到 1 的概率为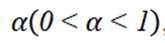
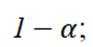
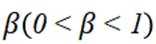
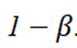
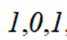
A采用单次传输方案, 若依次发送
B采用三次传输方案, 若发送1 ,则依次收到
C采用三次传输方案, 若发送1 ,则译码为 1 的概率为
D当 
正确答案
已知向量a,b满足|a−b|=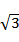
正确答案
底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为2,高为3的正四棱锥,所得棱台的体积为
正确答案
28
已知直线x−my+1=0与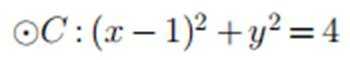
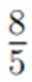
正确答案
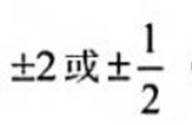
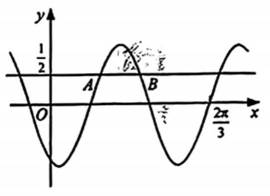
已知函数f(x)=sin(ωx+φ),如图,A,B是直线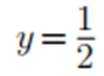
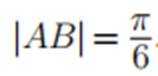
正确答案
记△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC面积为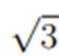
( 1 ) 若∠ADC=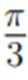
( 2 ) 若b2+c2=8,求b,c
正确答案
（1）
(2) 在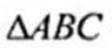
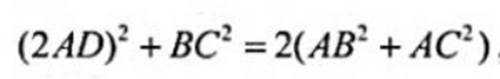
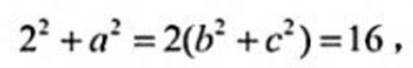
又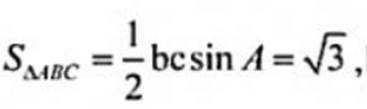
又由余弦定理得：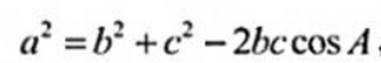
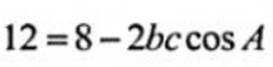
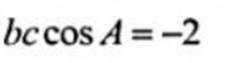
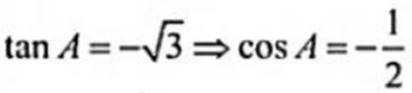
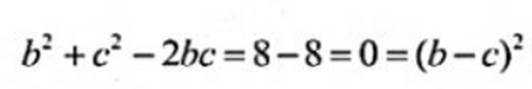
已知 {an}为等差数列,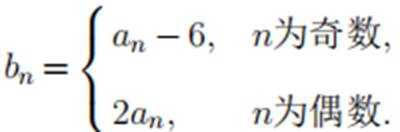 
( 1 ) 求{an}的通项公式;
( 2 ) 证明:当n>5时,Tn>Sn
正确答案
（1）
（2）由（1）知，
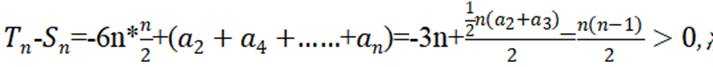
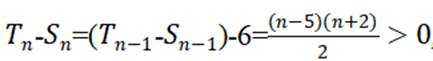
综上，当 n > 5 时, Tn > Sn
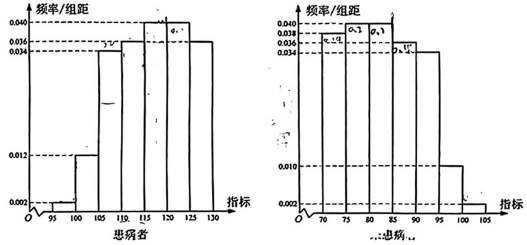
某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异, 经过大量调查, 得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准, 需要确定临界值 c, 将该指标大于 c 的人判定为阳性,
小于或等于 c 的人判定为阴性. 此检测标准的漏诊率是将患病者判定为阴性的概率,
记为 p(c); 误诊率是将未患病者判定为阳性的概率, 记为 q(c). 假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率
( 1 ) 当漏诊率 p(c) = 0.5% 时, 求临界值 c 和误诊率 q(c);
( 2 ) 设函数 f(c) = p(c) + q(c), 当 c ∈ [95, 105] 时, 求 f(c) 的解析式, 并求 f(c) 在区间[95, 105] 的最小值.
正确答案
（1）
（2）0.012
解析
（1）由题意当
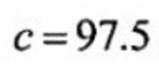
（2）当
当
所以，当C=100时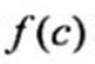
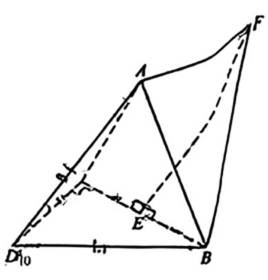
如图, 三棱锥 A − BCD 中, DA = DB = DC, BD ⊥ CD, ∠ADB = ∠ADC = 60 ◦ , E
为 BC 的中点
( 1 ) 证明: BC ⊥ DA;
( 2 ) 点 F 满足
正确答案
（1）证明：在棱锥A-BCD中,由于DA=DB=DC且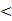
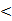
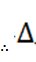
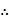
由于E是BC中点，链接DE，AE，则在等腰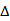
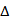
DE⊥BC,且
得BC⊥平面ADE,AD⊥平面ADE
得BC ⊥ DA
（2）由已知BD⊥CD
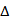
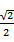
又∵
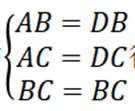
不妨设DB=DC=DA=2,则BC=2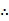
在
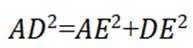
以E为原点，ED,EB,EA分别为x,y,z轴建立空间直角坐标系
则
由已知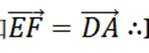
则
设平面ABD的法向量为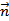
设平面ABF的法向量为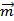
设二面角D-AB-F的平面角为
则|cos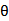
则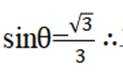
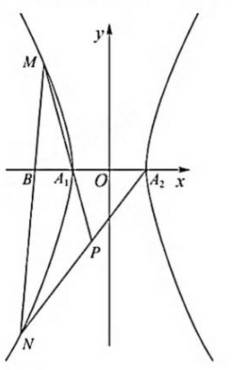
已知双曲线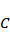 
(1) 求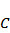 
(2) 记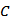 
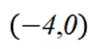
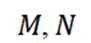
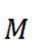
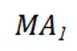
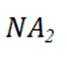
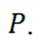
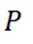
正确答案
( 1 )由题意,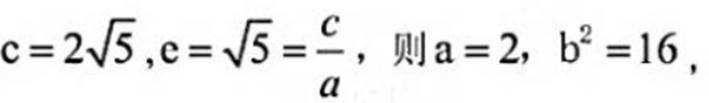
双曲线为
( 2 ) 设过点B的直线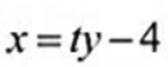
则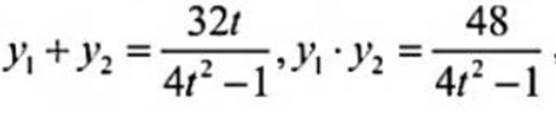
设直线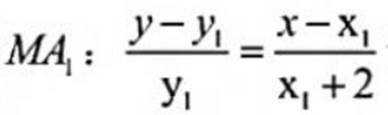
带入韦达定理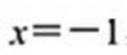
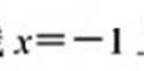
((1) 证明: 当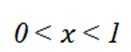 
（2）已知函数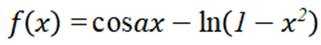 
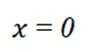
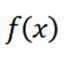
正确答案
( 1 ) 令g(x)=x-x2-sinx
g'(x)=1—2x—cosx,
g"(x)=-2+sinz<0,可知g'(x)在(0,1)上单调递减
∴g(x)<(0)=0,可知g(x)在(0,1)上单调递减
∴g(x)
∴x-x²
令h(x)=sinx-x
h'(x)=cosx-1≤0,可知h(x)在(0,1)上单调递减
∴h(x)
∴sinx
∴当0
(2)f'(x) =-asinax +
f"(x)=-a2cosax+
∵x=0为f(x)的极大值点
∴f"(0)<0
∴-a2+2<0
