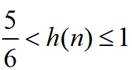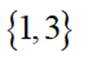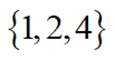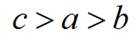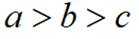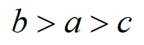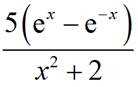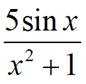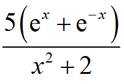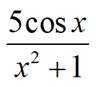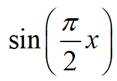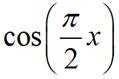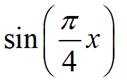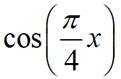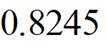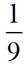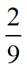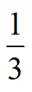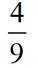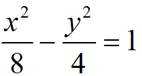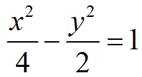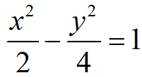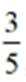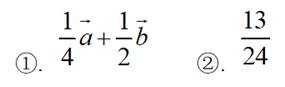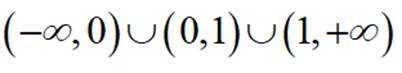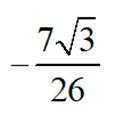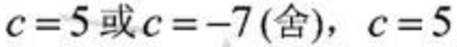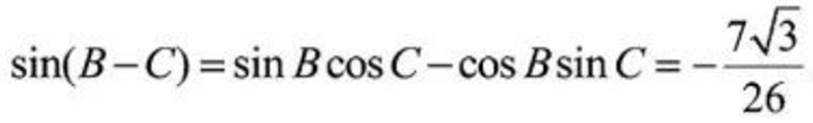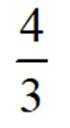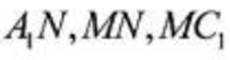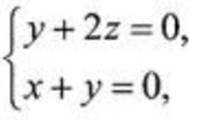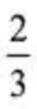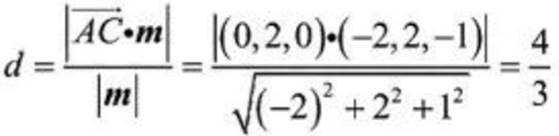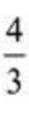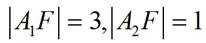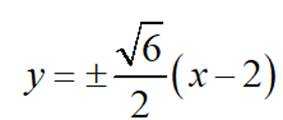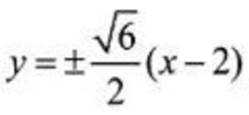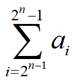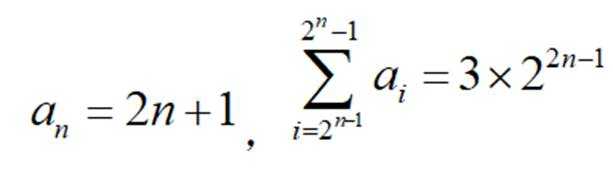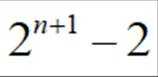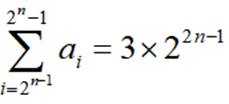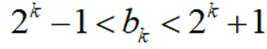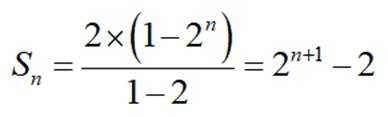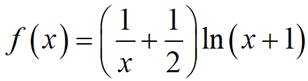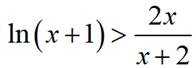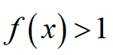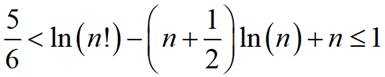已知集合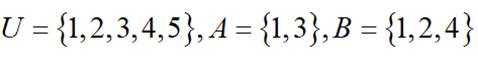
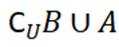
正确答案
“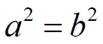
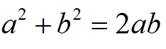
正确答案
若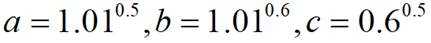
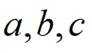
正确答案
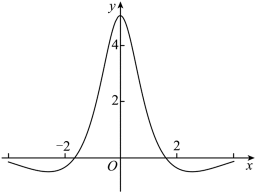
函数
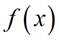
正确答案
已知函数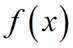
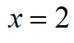
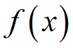
正确答案
已知
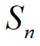

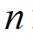
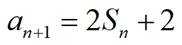
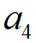
正确答案
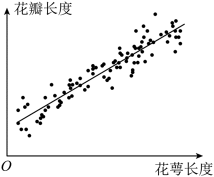
调查某种群花萼长度和花瓣长度,所得数据如图所示,其中相关系数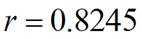
正确答案
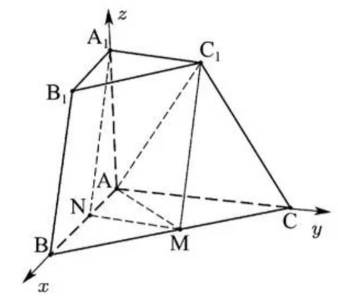
在三棱锥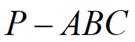
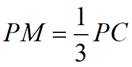
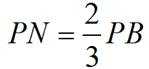
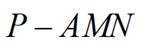

正确答案
双曲线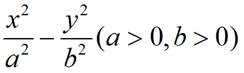
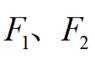
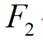
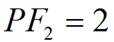
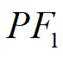
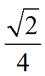
正确答案
已知i是虚数单位,化简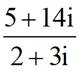
正确答案
4+i
在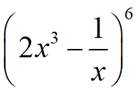
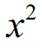
正确答案
60
过原点的一条直线与圆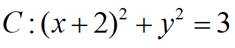
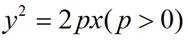
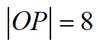
正确答案
6
甲乙丙三个盒子中装有一定数量的黑球和白球,其总数之比为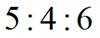
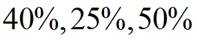
正确答案
(1)0.05 (2)
在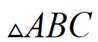

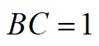
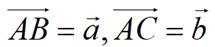
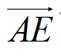
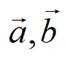
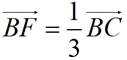
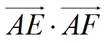
正确答案
若函数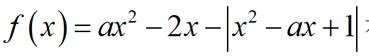
正确答案
在
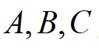

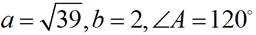
(1)求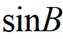
(2)求c的值;
(3)求
正确答案
(1)
解析
因为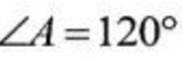
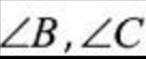

(1)由正弦定理得: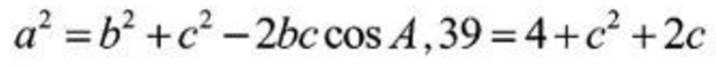
(2)由余弦定理得: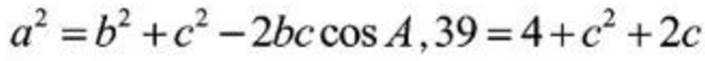

(3)因为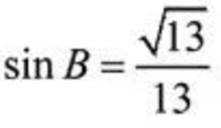
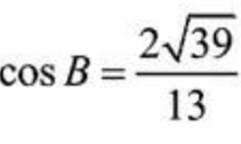

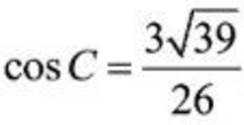
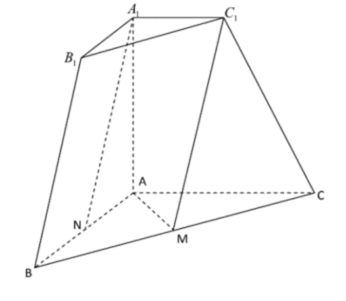
三棱台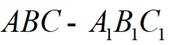
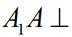
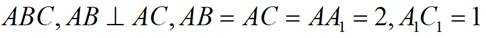
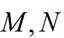
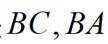
(1)求证: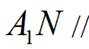
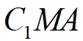
(2)求平面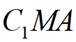

(3)求点C到平面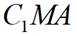
正确答案
(1)证明见解析(2)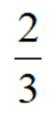
解析
(1)连接
因为N为线段AB的中点,M为线段BC的中点,所以线段MN是
所以
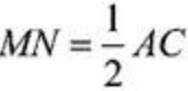
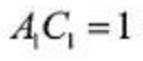
即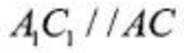
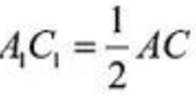
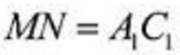

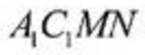
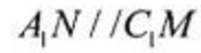
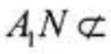


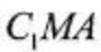

(2)因为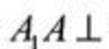

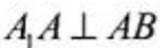
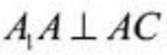
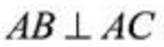
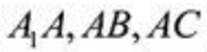
如图,以向量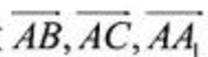
因为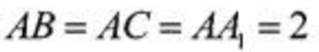
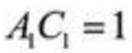
则A(0,0,0),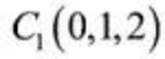
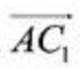
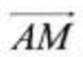
设平面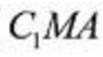
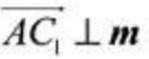
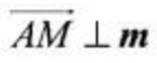
即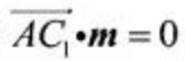

令y=2,则x=-2,z=-1,即m=(-2,2,-1),故平面

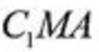
则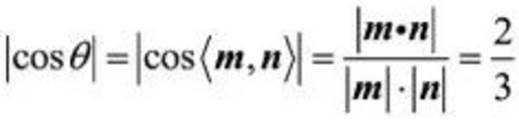
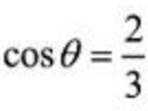
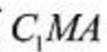
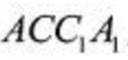
(3)由(2)知,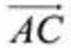
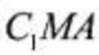
设点C到平面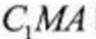
所以,点C到平面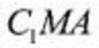
设椭圆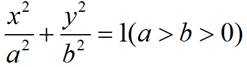
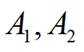
(1)求椭圆方程及其离心率;
(2)已知点P是椭圆上一动点(不与端点重合),直线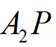
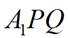

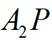
正确答案
(1)椭圆的方程为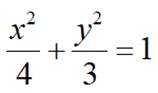
(2)
解析
(1)设糊圆C的焦距为2c(c> 0),则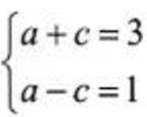
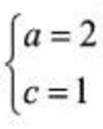

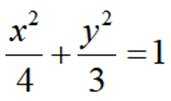
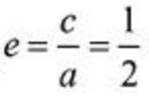
(2)由(1)可得,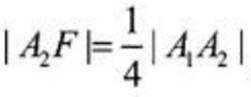
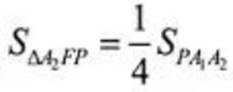
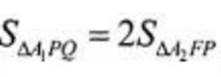
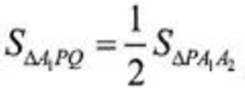
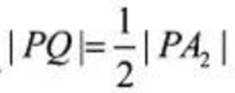
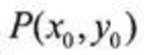
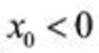
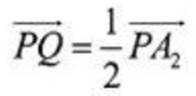
当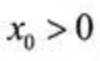
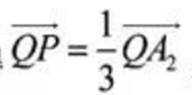
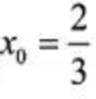
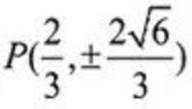
所以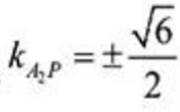
已知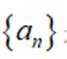
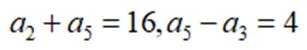
(1)求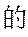
(2)已知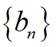
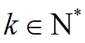
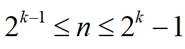
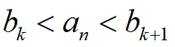
(Ⅰ)当
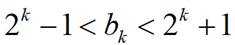
(Ⅱ)求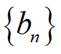
正确答案
(1)
(2)(Ⅰ)证明见解析;(Ⅱ)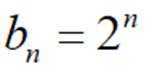
解析
(1)由题意得到关于首项、公差的方程,解方程可得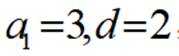
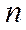
(2)(Ⅰ)利用题中的结论分别考查不等式两侧的情况,当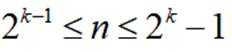
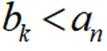
取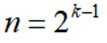
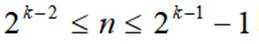
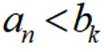
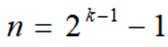
(Ⅱ)结合(Ⅰ)中的结论猜想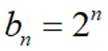
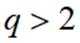
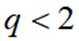
(1)由题意可得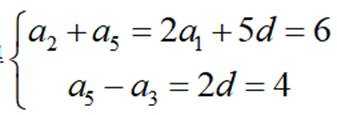
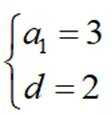
则数列
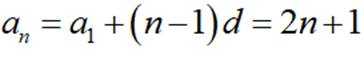
注意到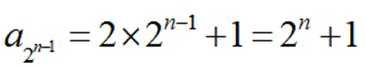
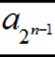

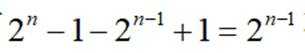
故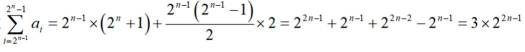
小问2详解
(Ⅰ)由题意可知,当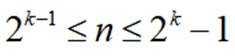
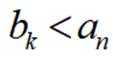
取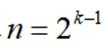
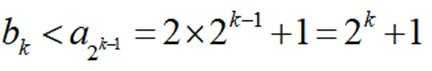
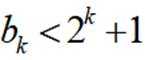
当
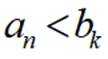
取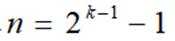
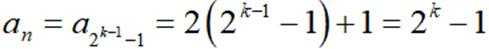
据此可得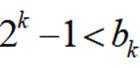
综上可得:
(Ⅱ)由(Ⅰ)可知: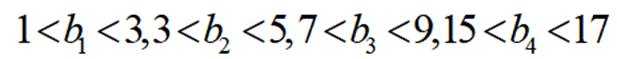
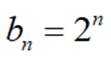
否则,若数列的公比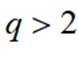
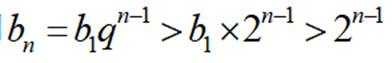
注意到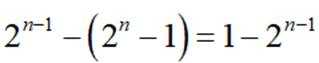
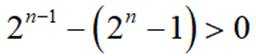
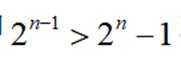
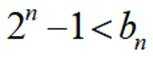
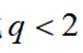
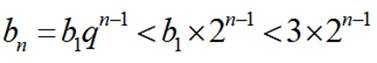
注意到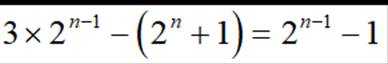
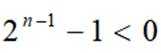
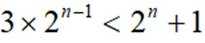

综上,数列的公比为2,则数列的通项公式为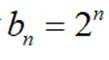
其前n项和为:
已知函数
(1)求曲线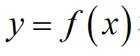
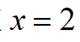
(2)当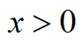
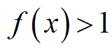
(3)证明: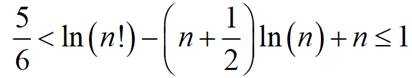
正确答案
(1)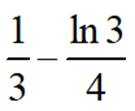
解析
(1)利用导数的几何意义求斜率;
(2)问题化为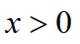
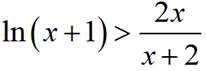

(3)构造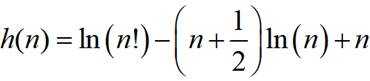
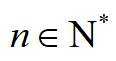
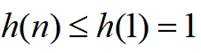
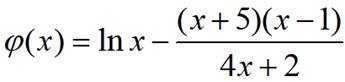
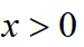
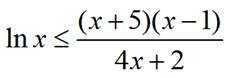
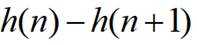
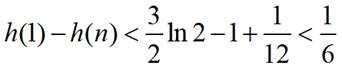
小问1详解
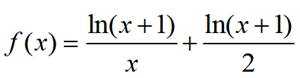
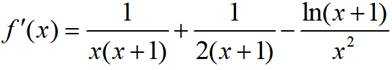
所以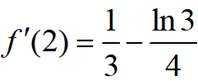
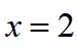
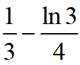
小问2详解
要证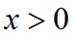
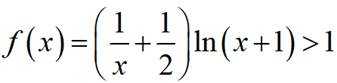
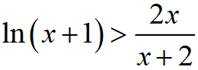
令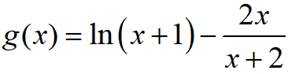
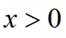
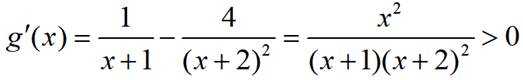
所以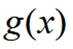

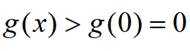
所以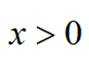
小问3详解
设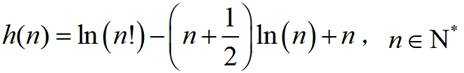
则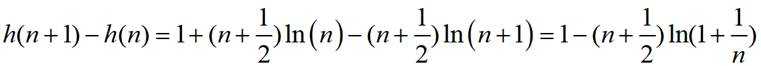
由(2)知: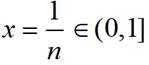
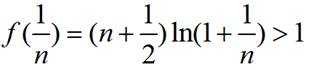
所以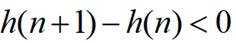
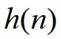
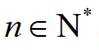
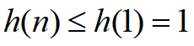
下证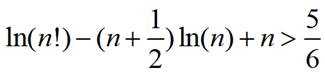
令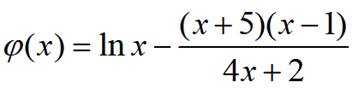
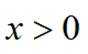

当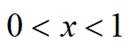
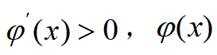
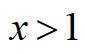
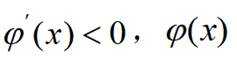
所以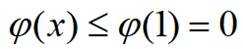
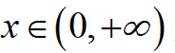
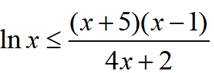
则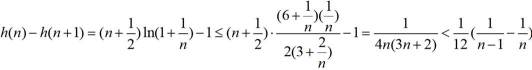
所以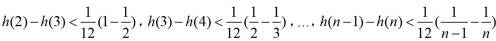
累加得: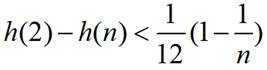
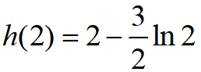
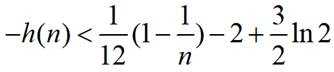
所以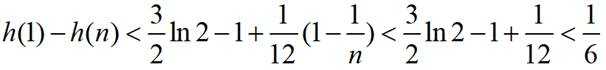
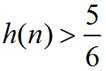
综上,