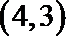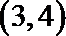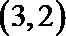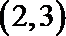1.已知集合
正确答案
解析

考查方向
本题主要考查集合的补集、交集运算
解题思路
1、求出B在R中的补集;
2、求出交集,即可得到结果。
易错点
本题易在求补集时发生错误,易忽视2。
知识点
2.已知向量
正确答案
解析
由向量


考查方向
本题主要考查了平面向量的平行关系。
解题思路
本题考查平面向量的平行关系,解题步骤如下:利用平行的坐标公式求解。
易错点
本题必须注意坐标表示。
知识点
4.计算:
正确答案
3
解析
分子、分母同除以3n+1,可求得极限为3。
考查方向
本题主要考查了极限的知识
解题思路
本题考查极限,解题步骤如下:利用极限的运算法则求解。
易错点
本题必须注意极限的运算法则。
知识点
6.
正确答案
解析
由题可知,T8=C107(2x)3=960x3,可求得T8=
考查方向
本题主要考查了二项式定理。
解题思路
本题考查二项式定理,解题步骤如下:利用通项公式求解。
易错点
本题要注意通项公式。
知识点
7.某船在海平面








正确答案
解析
由题可知,AB=6,AC=8.1,A=30o,可求得BC=
考查方向
本题主要考查了解三角形的实际应用举例。
解题思路
本题考查余弦定理,解题步骤如下:利用余弦定理求解。
易错点
本题要注意余弦定理。
知识点
11.有一列向量






正确答案

解析
由题可知,差向量为(1,1),则向量an=(-21+n,12+n)。所以|an|2=(-21+n)2+(12+n)2=2n2-18n+585,则当n=4或5时取到最小值。
考查方向
本题主要考查了向量的模及新定义。
解题思路
本题考查向量的模,按照定义求解。
易错点
本题要注意按照定义求解。
知识点
5.若复数


正确答案
解析
由题可知,z=i(1-2i)=2+i,可求得
考查方向
本题主要考查了行列式与复数的运算。
解题思路
本题考查行列式与复数的运算,解题步骤如下:利用行列式及复数的运算法则求解。
易错点
本题必须注意行列式的运算法则。
知识点
8.已知
正确答案
解析
由题可知,sina=3/5,可求得cosa=4/5,所以
考查方向
本题主要考查了两角和差公式和诱导公式
解题思路
本题考查两角和差公式和诱导公式,解题步骤如下:利用两角和差公式和诱导公式求解。
易错点
本题要注意诱导公式。
知识点
9.如图,已知正方体








正确答案
解析
由题可知,BE=

考查方向
本题主要考查了立体几何的线面角。
解题思路
本题考查立体几何的线面角,解题步骤如下:连接BE,则∠AEB为所求线面角,解三角形即可。
易错点
本题要注意作辅助线。
知识点
10.已知函数




①
②

③

④

其中正确命题的序号为________(写出所有正确命题的序号)。
正确答案
②③
解析
由题可知,f(x)=log2x,h(x)=log2(1-|x|),作出h(x)的图像,观察图像可得结论: ②③正确。
考查方向
本题主要考查了函数的图像性质。
解题思路
本题考查函数的图像性质,解题步骤如下:求出f(x),h(x),利用图像观察性质。
易错点
本题要注意反函数的性质。
知识点
12.已知


正确答案
17
解析
本题主要考查了函数的图像求交点。
考查方向
本题主要考查了函数的图像求交点。
解题思路
本题考查函数图像求交点,分别作出f(x),g(x)的图像求解。
易错点
本题要注意利用图像求解。
知识点
25.已知






正确答案
略
解析
试题分析:本题属于立体几何中的基本问题,题目为容易题.
证明:在


又因为

所以四边形
所以
又因为


考查方向
本题考查了立体几何中的线面平行的问题.属于高考中的高频考点。
解题思路
本题考查线面平行,解题步骤如下:
找出平行四边形即可
易错点
容易与线面垂直混淆。
知识点
27.已知两个向量
(1)若

(2)求函数
正确答案


解析
试题分析:本题属于向量和对数函数中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求
(2)要注意转化后的定义域.
(1)
经检验
(2)由条件知
所以值域为
考查方向
本题考查了向量和对数函数的知识
解题思路
本题考查向量和对数函数,解题步骤如下:
1、利用向量垂直化简求解。
2、利用换元法转化为二次函数求解。
易错点
利用换元法时容易出错。
知识点
30.如图,点















正确答案
解析
试题分析:本题属于圆锥曲线中的偏难问题,题目的难度较大,
(1)直接按照步骤来求
(2)要注意对参数的讨论.
存在一条双曲线,对任意的正整数

如图所示,





所以
当

所以

当且仅当
故


考查方向
本题考查了直线与圆锥曲线的位置关系,属于高考中的高频考点.
解题思路
本题考查圆锥曲线与直线的位置关系,表示出直线斜率依次求解。
易错点
表示直线斜率时容易出错。
知识点
31.定义符号函数
(1)求


(2)当



(3)已知存在



正确答案



解析
试题分析:本题属于函数中较难的问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求
(2)要注意转化后的定义域.
(1)
所以

(2)当



所以由
令

由图像可得
(3)当



所以


即

从而只需求







对于函数

(i)
(ii)
(iii)
综上,
考查方向
本题考查了绝对值函数及零点的知识.
解题思路
本题考查绝对值函数,解题步骤如下:
1、利用定义表示函数求解。
2、利用函数图像求解。
3、利用分类讨论求解。
易错点
利用定义表示函数时容易出错。
知识点
26.已知函数





正确答案


解析
试题分析:
本题属于三角函数中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求
(2)要注意公式的应用
由


再把横坐标缩短到原的

由
所以
考查方向
本题考查了三角函数图像变换的知识,涉及到图像性质,是高考题中的高频考点
解题思路
本题考查三角函数图像变换,解题步骤如下:
1、利用伸缩平移变换化简。
2、利用公式代入求解。
易错点
平移变换时容易出错。
知识点
28.已知数列


(1)求

(2)当


正确答案
an=3n-2;
解析
(1)

当
(2)
设



考查方向
本题主要考查数列的综合运算
解题思路
1、求出an;
2、利用公式分离出λ,即可得到结果。
易错点
本题易在分离λ时发生错误。
知识点
29.在平面直角坐标系





(1)设椭圆




(2)设点









(3)已知直线

















正确答案
(1)
(2)
(3)
(1)由点

由题意

又

(也可以先求出

(2)假设存在实数
由题意
于是


只要
故存在实数



(学生通过联想,判断直线



(3)设




又

所以
综上
解析
试题分析:本题属于圆锥曲线中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求
(2)要注意对参数的讨论.
考查方向
本题考查了直线与椭圆的位置关系,属于高考中的高频考点
解题思路
本题考查圆锥曲线与直线的位置关系,解题步骤如下:
1、利用新定义求解。
2、联立直线与椭圆方程求解。
易错点
第二问中表示直线斜率时容易出错。
知识点
32.已知两个无穷数列






(1)若数列

(2)若数列





①若数列

②若数列






正确答案
an=2n-1; 



解析
(1)数列


∴

(2)①∵数列



∴数列

故
② ∵

而数列



假设存在正整数





i.当
当



ii.当
显然不存在

iii.当
当


所以
当




此时



考查方向
本题主要考查数列的综合运算
解题思路
1、求出an,bn;
2、利用定义求解,即可得到结果。
易错点
本题易在利用新定义求解时发生错误。
知识点
3.关于

正确答案
解析
由题可知,系数矩阵为
考查方向
本题主要考查了矩阵的知识。
解题思路
本题考查系数矩阵,解题步骤如下:利用矩阵的概念求解。
易错点
本题必须注意矩阵的概念。
知识点
13.如果
正确答案
解析
若a=1,b=2带入验证可得正确选项。A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
本题主要考查不等式的基本性质
解题思路
本题可依次代入特殊值逐一验证排除。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在代特殊值时发生错误。
知识点
14.设




正确答案
解析
由题可知,易得由x=1且y=2可推出x+y=3,反之不成立。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查简易逻辑
解题思路
本题直接判断,即可得到结果。
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在前后互推判断时发生错误。
知识点
16.甲、乙、丙、丁四人排成一排,其中甲、乙两人相邻的概率是
正确答案
解析
由A44=24,A22*A33=12,则P=
考查方向
本题主要考查排列组合、概率计算
解题思路
1、求出4人排队的总方法数;
2、求出甲乙相邻的方法数,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在求方法数时发生错误。
知识点
15.方程


正确答案
解析
由
考查方向
本题主要考查椭圆的标准方程
解题思路
1、把方程化为标准形式;
2、利用a>b判断。
易错点
本题易在判断a,b>0时发生错误。
知识点
21.已知函数
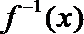
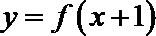
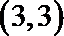
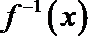
正确答案
解析
由f(x)恒过(4,3)得函数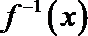
考查方向
本题主要考查反函数及图像平移
解题思路
1、求出f(x)所过定点;
2、利用对称性求解,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在代点时发生错误。
知识点
17.直线

正确答案
解析
由题可知,圆心
考查方向
本题主要考查直线与圆的位置关系。
解题思路
1、求出圆心和半径;
2、利用点到直线的距离公式求解,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在利用点到直线的距离公式时发生错误。
知识点
18.某人5次上班途中所花的时间(单位:分钟)分别为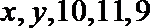
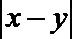
正确答案
解析
x+y+30=50,(x-10)2+(y-10)2+1+1=10,解得(x-y)2=16。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查统计
解题思路
1、表示出平均数和方差;
2、联立解方程,即可得到结果。
易错点
本题易在求方差时发生错误。
知识点
19.设函数



正确答案
解析

考查方向
本题主要考查三角函数求值
解题思路
1、表示出
2、按照题目条件依次代入,即可得到结果。
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在代值计算时发生错误。
知识点
20.如果底面直径和高相等的圆柱的侧面积是
正确答案
解析
由S=h*πh,则V= h*πh2/4=
考查方向
本题主要考查圆柱的体积
解题思路
1、利用S表示高和底面半径;
2、代入体积公式,即可得到结果。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在求高时发生错误。
知识点
24.将一圆的六个等分点分成两组相间的三点,它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星,如图所示的正六角星的中心为点





正确答案
解析
因为想求
①因为

②因为

③因为

④因为
所以
⑤因为

⑥因为

因此,

考查方向
本题主要考查向量的加法减法运算及几何意义
解题思路
表示向量,利用向量加法运算法则讨论,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在表示向量时发生错误。
知识点
22.一个弹性小球从10米自由落下,着地后反弹到原来高度的

正确答案
解析
由an=10(

考查方向
本题主要考查等比数列求和
解题思路
1、求出an;
2、利用Sn的公式求解,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在求和时发生错误。
知识点
23.符合以下性质的函数称为“
①定义域为
②
③

④

⑤对任意一个小于



下列四个函数中




正确答案
解析
由新定义依次对每个函数逐一判断,得出结论。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
主要考查函数的性质
解题思路
利用已知定义依次判断,即可得到结果。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在判断函数性质时发生错误。