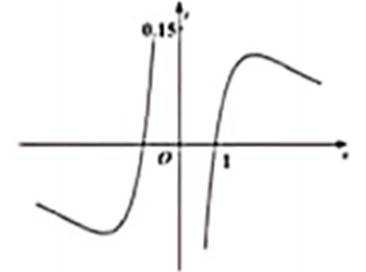
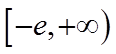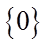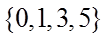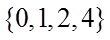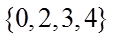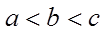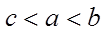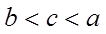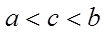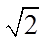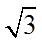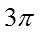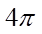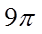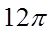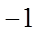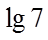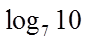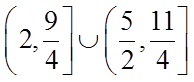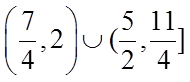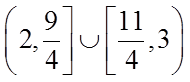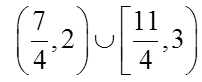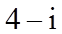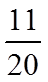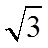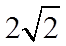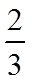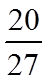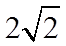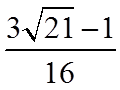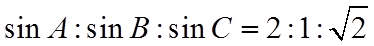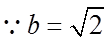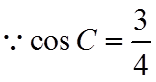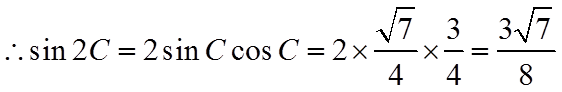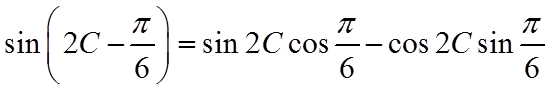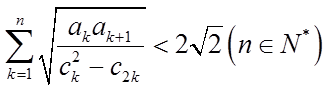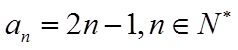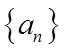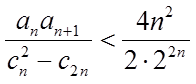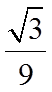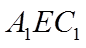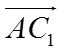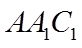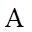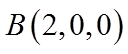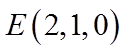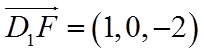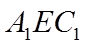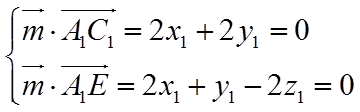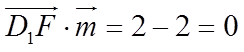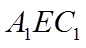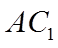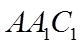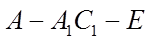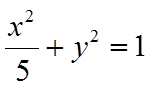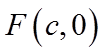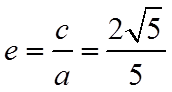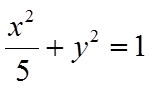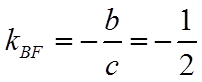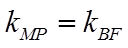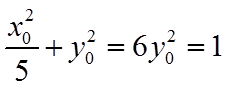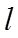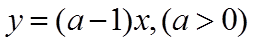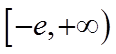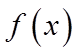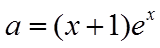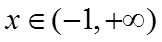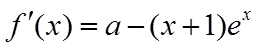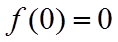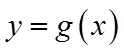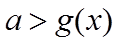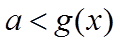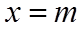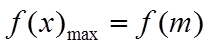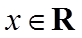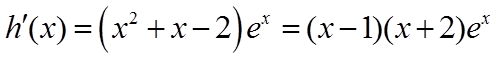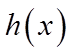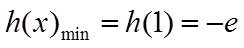1.设集合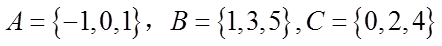
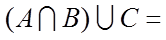
正确答案
5.设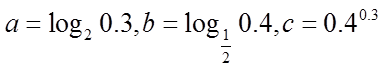
正确答案
8.已知双曲线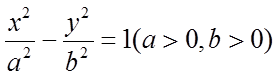
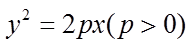
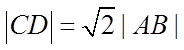
正确答案
2.已知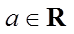
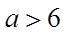
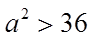
正确答案
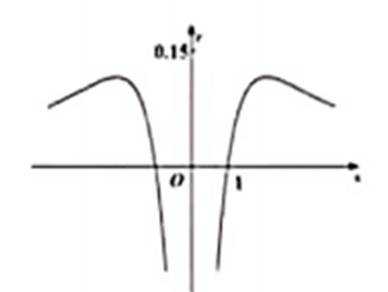
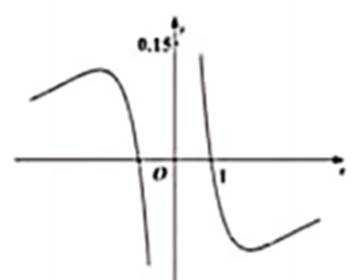
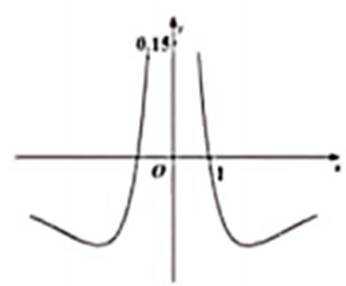
3.函数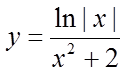
正确答案
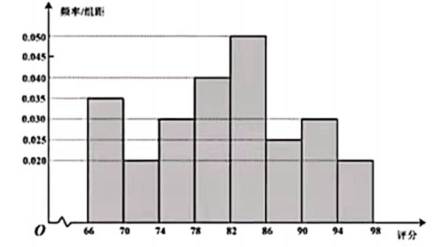
4.从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组: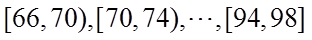
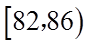
正确答案
6.两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为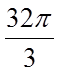
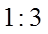
正确答案
7.若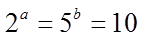
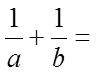
正确答案
9.设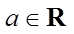
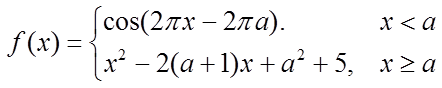
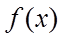
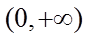
正确答案
10.i是虚数单位,复数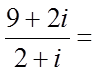
正确答案
11.在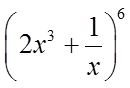
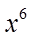
正确答案
160
15.在边长为1的等边三角形ABC中,D为线段BC上的动点,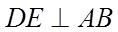
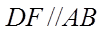
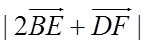
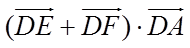
正确答案
①. 1 ②.
12.若斜率为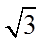
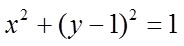
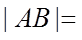
正确答案
13.若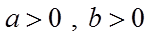
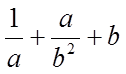
正确答案
14.甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局.已知每次活动中,甲、乙猜对的概率分别为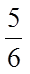
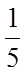
正确答案
①. 
16.(本小题满分14分)
在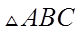
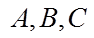
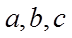
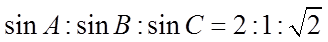
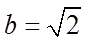
(I)求a的值;
(II)求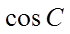
(III)求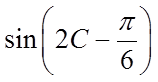
正确答案
(I)
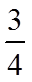
解析
(I)由正弦定理可得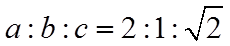
(II)由余弦定理即可计算;
(III)利用二倍角公式求出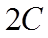
【详解】(I)因为
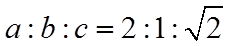

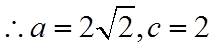
(II)由余弦定理可得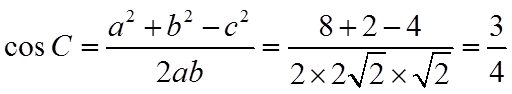
(III)
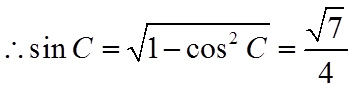

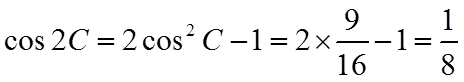
所以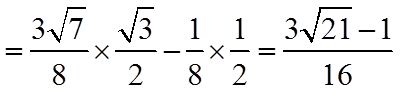
19.(本小题满分15分)
已知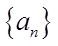
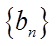
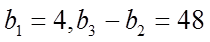
(I)求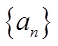
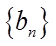
(II)记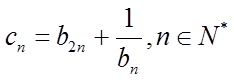
(i)证明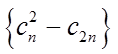
(ii)证明
正确答案
(I)
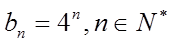
解析
(I)由等差数列的求和公式运算可得
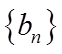
(II)(i)运算可得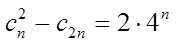
(ii)放缩得
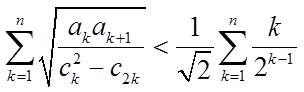
【详解】(I)因为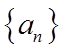
所以
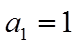
所以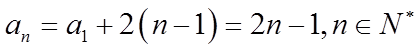
设等比数列
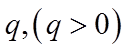
所以
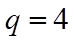
所以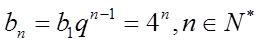
(II)(i)由题意,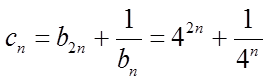
所以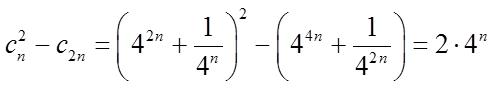
所以
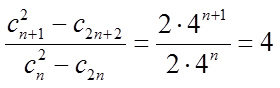
所以数列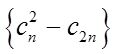
(ii)由题意知,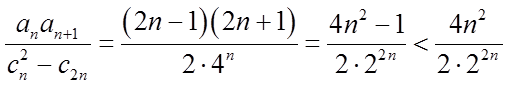
所以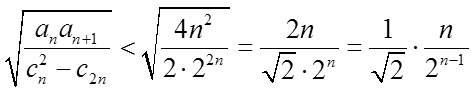
所以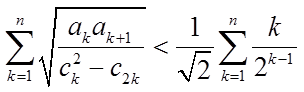
设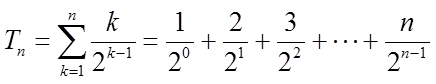
则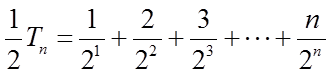
两式相减得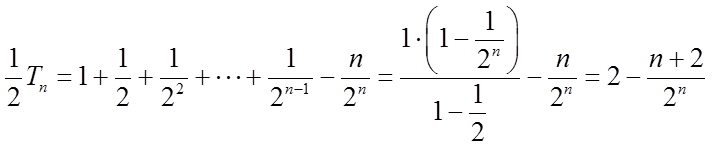
所以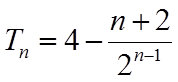
所以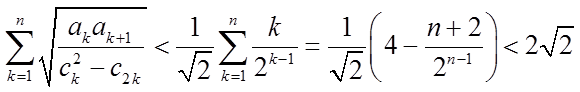
17.(本小题满分15分)
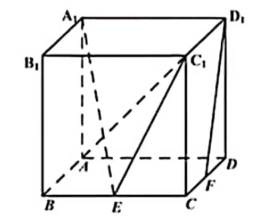
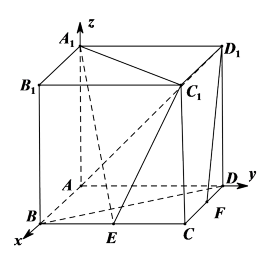
如图,在棱长为2的正方体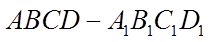
(I)求证: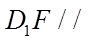
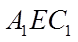
(II)求直线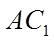
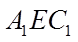
(III)求二面角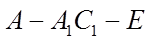
正确答案
(I)证明见解析;(II)
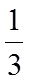
解析
(I)建立空间直角坐标系,求出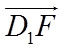

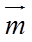
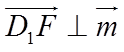
(II)求出
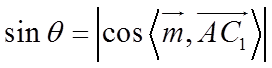
(III)求得平面
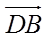
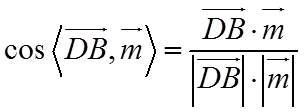
【详解】(I)以
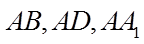
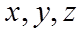
则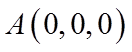
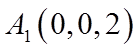

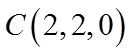
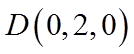
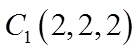
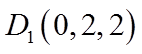
因为E为棱BC的中点,F为棱CD的中点,所以
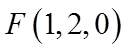
所以
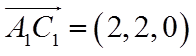
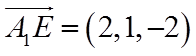
设平面
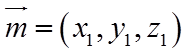
则
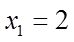
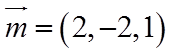
因为
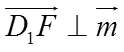
因为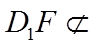

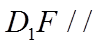
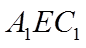
(II)由(1)得,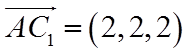
设直线
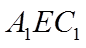
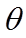
则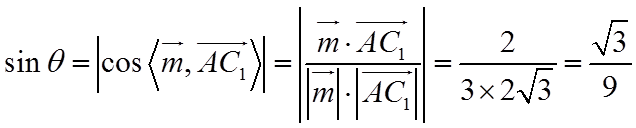
(III)由正方体的特征可得,平面
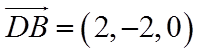
则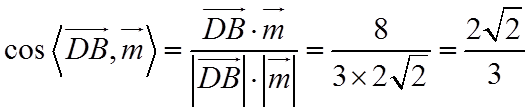
所以二面角
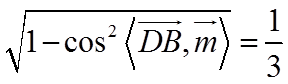
18.(本小题满分15分)
已知椭圆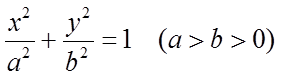
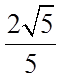
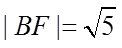
(I)求椭圆的方程;
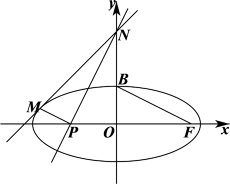
(II)直线l与椭圆有唯一的公共点M,与y轴的正半轴交于点N,过N与BF垂直的直线交x轴于点P.若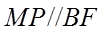
正确答案
(1)
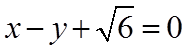
解析
(1)求出
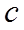
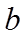
(2)设点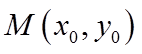
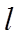
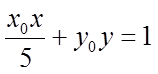

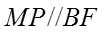
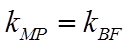
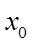
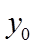
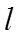
【详解】(1)易知点
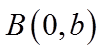
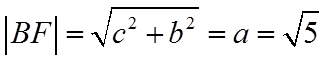
因为椭圆的离心率为
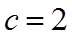
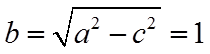
因此,椭圆的方程为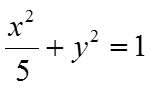
(2)设点
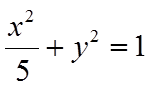
先证明直线
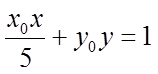
联立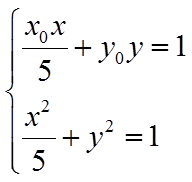

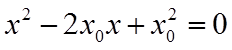
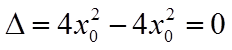
因此,椭圆
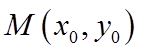
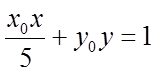
在直线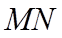

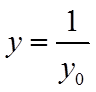
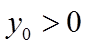
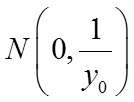
直线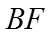

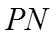
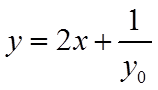
在直线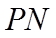

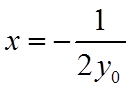
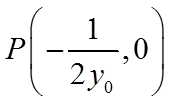
因为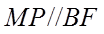

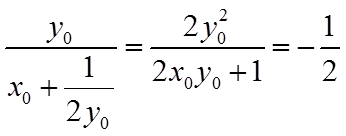
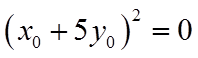
所以,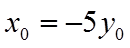

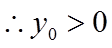
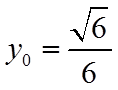
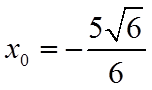
所以,直线
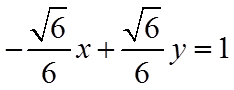
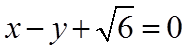
20.(本小题满分16分)
已知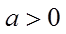
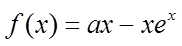
(I)求曲线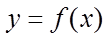
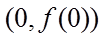
(II)证明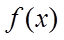
(III)若存在a,使得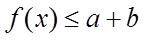
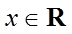
正确答案
(I)
解析
(I)求出
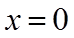
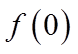
(II)令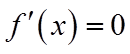

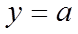
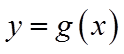
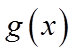
(III)令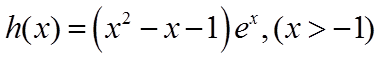

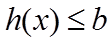
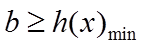
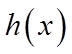
【详解】(I)
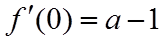
又
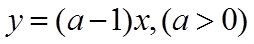
(II)令
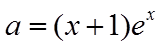
令
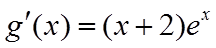
当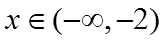
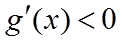

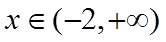
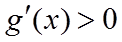
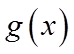
当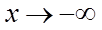
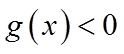

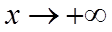
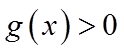
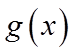
所以当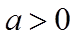
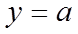

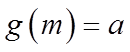
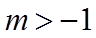
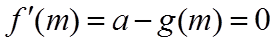
当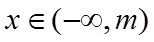

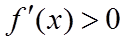
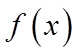
当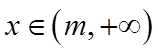

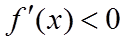
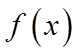

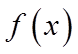
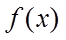
(III)由(II)知
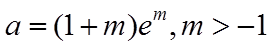
所以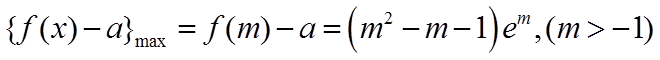
令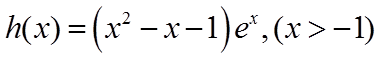
若存在a,使得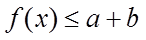

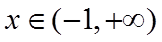
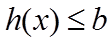
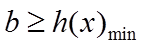

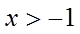
当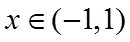
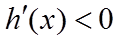

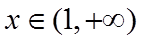
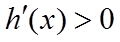
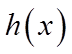
所以
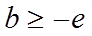
所以实数b的取值范围