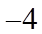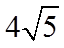1. 已知集合


正确答案
解析
结合题意利用并集的定义计算即可.
【详解】由题意可得:

故选:B.
2. 在复平面内,复数


正确答案
解析
由题意利用复数的运算法则整理计算即可求得最终结果.
【详解】由题意可得:
故选:D.
3. 已知






正确答案
解析
利用两者之间的推出关系可判断两者之间的条件关系.
【详解】若函数




若


比如
但


故




故“函数




故选:A.
4. 某四面体的三视图如图所示,该四面体的表面积为( )
正确答案
解析
根据三视图可得如图所示的几何体(三棱锥),根据三视图中的数据可计算该几何体的表面积.
【详解】根据三视图可得如图所示的几何体-正三棱锥
其侧面为等腰直角三角形,底面等边三角形,
由三视图可得该正三棱锥的侧棱长为1,
故其表面积为
故选:A.
5. 双曲线


正确答案
解析
分析可得


【详解】



将点



因此,双曲线的方程为
故选:A.
6. 






正确答案
解析
由已知条件求出

【详解】由已知条件可得


故选:B.
7. 函数
正确答案
解析
由函数奇偶性的定义结合三角函数的性质可判断奇偶性;利用二倍角公式结合二次函数的性质可判断最大值.
【详解】由题意,
又
所以当


故选:D.
8. 定义:24小时内降水在平地上积水厚度(




正确答案
解析
计算出圆锥体积,除以圆面的面积即可得降雨量,即可得解.
【详解】由题意,一个半径为


所以积水厚度
故选:B.
9. 已知圆





正确答案
解析
先求得圆心到直线距离,即可表示出弦长,根据弦长最小值得出
【详解】由题可得圆心为
则圆心到直线的距离
则弦长为
则当


故选:C.
10. 数列



正确答案
解析
使数列首项、递增幅度均最小,结合等差数列的通项及求和公式即可得解.
【详解】若要使n尽可能的大,则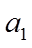
不妨设数列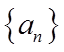
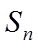
则
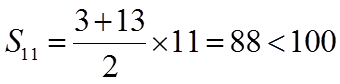
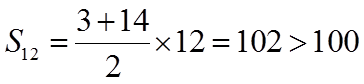
所以n的最大值为11.
故选:C.
第二部分(非选择题共110分)
11. 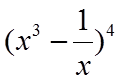
正确答案
解析
【详解】试题分析: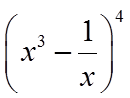
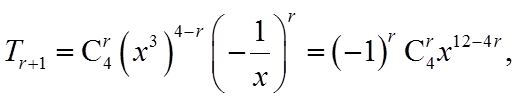

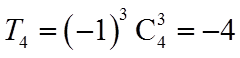
教师点评
二项式定理.
12. 已知抛物线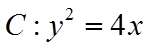
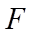
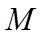
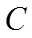
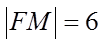
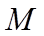
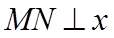
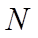
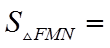
正确答案
①. 5 ②.
解析
根据焦半径公式可求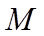
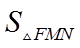
【详解】因为抛物线的方程为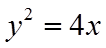
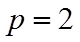
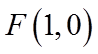
因为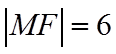
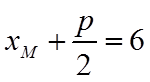
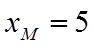
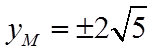
所以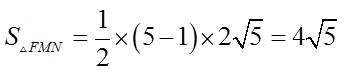
故答案为:5,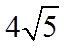
13. 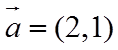
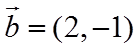
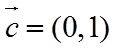
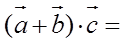
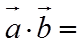
正确答案
①. 0 ②. 3
解析
根据坐标求出
【详解】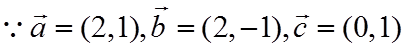
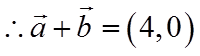

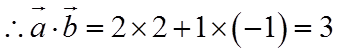
故答案为:0;3.
14. 若点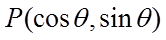
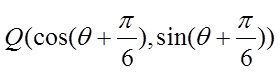
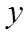
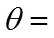
正确答案
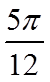
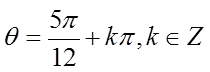
解析
根据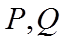
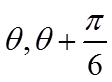
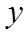

【详解】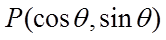
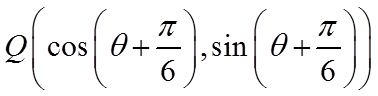
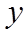
即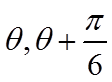
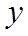
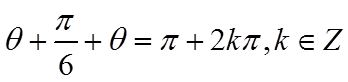
则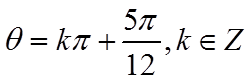
当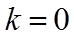
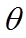
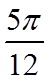
故答案为: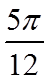
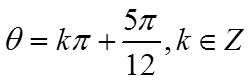
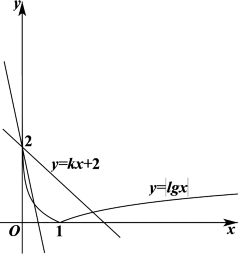
15. 已知函数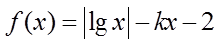
①若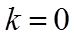
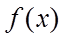
②
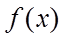
③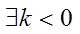
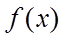
④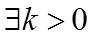
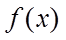
以上正确结论得序号是_______.
正确答案
①②④
解析
由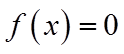
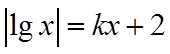
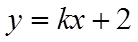
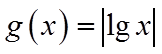
【详解】对于①,当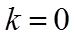
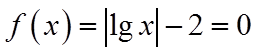
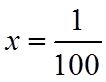
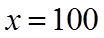
对于②,考查直线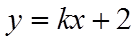
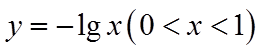
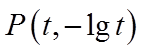
对函数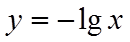
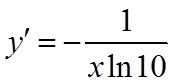
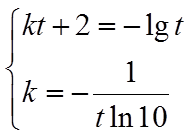
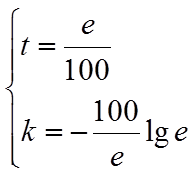
所以,存在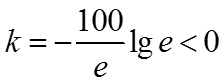
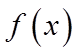
对于③,当直线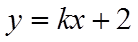
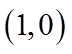
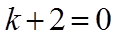
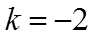
所以,当
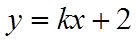
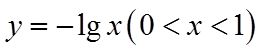
若函数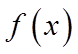
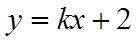
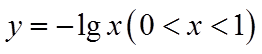
直线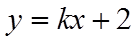
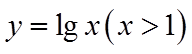
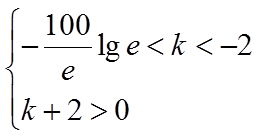
因此,不存在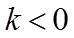

对于④,考查直线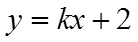
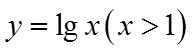
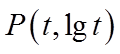
对函数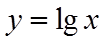
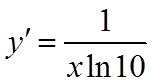
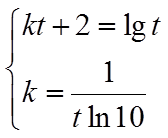
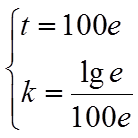
所以,当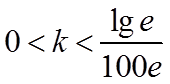
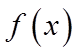
故答案为:①②④.
【点睛】思路点睛:已知函数的零点或方程的根的情况,求解参数的取值范围问题的本质都是研究函数的零点问题,求解此类问题的一般步骤:
(1)转化,即通过构造函数,把问题转化成所构造函数的零点问题;
(2)列式,即根据函数的零点存在定理或结合函数的图象列出关系式;
(3)得解,即由列出的式子求出参数的取值范围.
16. 已知在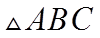
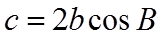
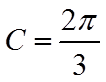
(1)求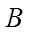
(2)在下列三个条件中选择一个作为已知,使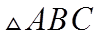
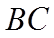
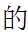
①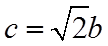
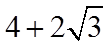
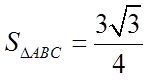
正确答案
(1)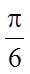
解析
(1)由正弦定理化边为角即可求解;
(2)若选择①:由正弦定理求解可得不存在;
若选择②:由正弦定理结合周长可求得外接圆半径,即可得出各边,再由余弦定理可求;
若选择③:由面积公式可求各边长,再由余弦定理可求.
【详解】(1)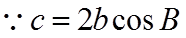
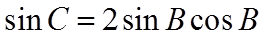
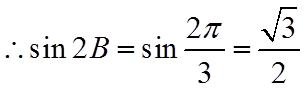
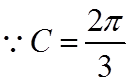
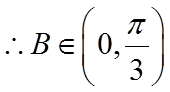


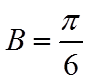
(2)若选择①:由正弦定理结合(1)可得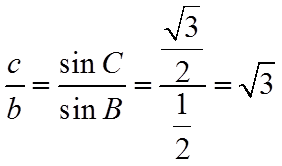
与
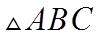
若选择②:由(1)可得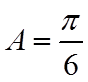
设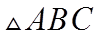
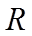
则由正弦定理可得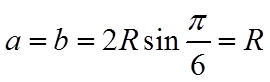
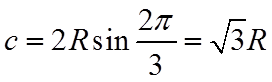
则周长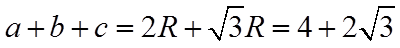
解得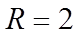
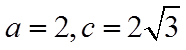
由余弦定理可得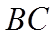
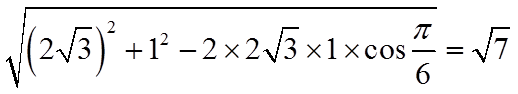
若选择③:由(1)可得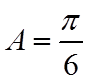
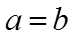
则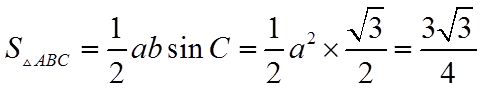
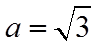
则由余弦定理可得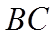
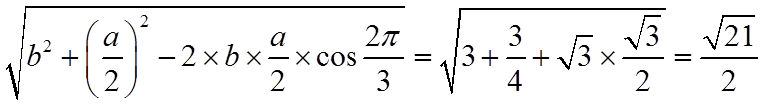
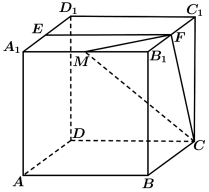
17. 已知正方体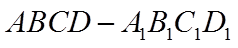
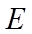
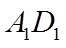
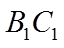
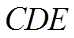
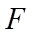
(1)证明:点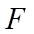

(2)若点


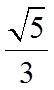

正确答案
(1)证明见解析;(2)
解析
(1)首先将平面

(2)建立空间直角坐标系,利用空间直角坐标系求得相应平面的法向量,然后解方程即可求得实数
【详解】(1)如图所示,取


由于


从而

据此可得:直线


当直线与平面相交时只有唯一的交点,故点

即点

(2)以点





不妨设正方体的棱长为2,设
则:
从而:
设平面


令

设平面


令

从而:
则:
整理可得:


【点睛】本题考查了立体几何中的线面关系和二面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力,对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.
18. 为加快新冠肺炎检测效率,某检测机构采取“k合1检测法”,即将k个人的拭子样本合并检测,若为阴性,则可以确定所有样本都是阴性的;若为阳性,则还需要对本组的每个人再做检测.现有100人,已知其中2人感染病毒.
(1)①若采用“10合1检测法”,且两名患者
②已知10人分成一组,分10组,两名感染患者在同一组的概率为
(2)若采用“5合1检测法”,检测次数Y的期望为E(Y),试比较E(X)和E(Y)的大小(直接写出结果).
正确答案
(1)①

解析
(1)①由题设条件还原情境,即可得解;
②求出X的取值情况,求出各情况下的概率,进而可得分布列,再由期望的公式即可得解;
(2)求出
【详解】(1)①对每组进行检测,需要10次;再对结果为阳性的组每个人进行检测,需要10次;
所以总检测次数为20次;
②由题意,


则
所以
(2)由题意,


则
若

若

若

19. 已知函数
(1)若


(2)若函数


正确答案
(1)






解析
(1)求出

(2)由


【详解】(1)当




此时,曲线



(2)因为

由题意可得

故

所以,函数



当



所以,

20. 已知椭圆


(1)求椭圆E的标准方程;
(2)过点P(0,-3)的直线l斜率为k,交椭圆E于不同的两点B,C,直线AB,AC交y=-3于点M、N,直线AC交y=-3于点N,若|PM|+|PN|≤15,求k的取值范围.
正确答案
(1)

解析
(1)根据椭圆所过的点及四个顶点围成的四边形的面积可求
(2)设






【详解】(1)因为椭圆过

因为四个顶点围成的四边形的面积为


故椭圆的标准方程为:
(2)
设
因为直线

故直线



直线


故


又

又
故

综上,
21. 定义






(1)对于前4项2,-2,0,1的数列,可以是
(2)若


(3)是否存在p,使得存在


正确答案
(1)不可以是


解析
(1)由题意考查

(2)由题意首先确定数列的前4项,然后讨论计算即可确定
(3)构造数列



【详解】(1)由性质③结合题意可知
矛盾,故前4项

(2)性质①
由性质③




若



若


因此只能是
又因为



若

不满足
当

下面用纳法证明
当

当
若



否则,若


而由性质②可得:

同理可得:






即当
综上可得:

(3)令

由于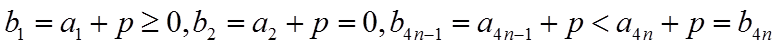
因此数列

由(2)可知:
若


因此


【点睛】本题属于数列中的“新定义问题”,“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变才是制胜法宝.