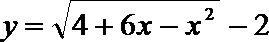2.下列说法中,正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.等差数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.有8张卡片分别标有数字1,2,3,4,5,6,7,8,从中取出6张卡片排成3行2列,要求3行中仅有中间行的两张卡片上的数字之和为5,则不同的排法共有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图,正方体


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.如图,AB,CD是半径为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在极坐标系



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.将函数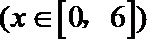
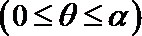
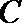


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知







正确答案

解析
解析已在路上飞奔,马上就到!
知识点
12.设


正确答案
(-∞,2)
解析
解析已在路上飞奔,马上就到!
知识点
15.设锐角三角形ABC的内角A、B、C的对边分别为



(Ⅰ)求
(Ⅱ)求
正确答案
(Ⅰ)由


由

(Ⅱ)

由



所以

所以,

解析
解析已在路上飞奔,马上就到!
知识点
16.某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上40件产品作为样本算出他们的重量(单位:克)重量的分组区间为(490,


(1)根据频率分布直方图,求重量超过505克的产品数量.
(2)在上述抽取的40件产品中任取2件,设Y为重量超过505克的产品数量,求Y的分布列.
(3)从流水线上任取5件产品,求恰有2件产品的重量超过505克的概率.
正确答案
(1)重量超过505克的产品数量是

(2)Y的分布列为
(3)
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,斜三棱柱





(Ⅰ)求证:平面

(Ⅱ)求证:
(Ⅲ)求二面角
正确答案
(Ⅰ)证明:设

在斜三棱柱


















解法一:(Ⅱ)连接










(Ⅲ)过点










设











在



∴

解法二:(Ⅱ)因为点













设

设





(Ⅲ)设平面

则


设平面

∴





解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数

(Ⅰ)若


(Ⅱ)求
(Ⅲ)若

正确答案
(Ⅰ)
∵

(Ⅱ)
∵


①当


②当
由
∴
(Ⅲ)当
当



综上可知,若


解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆C:


(I)求椭圆的方程;
(II)若直线


正确答案
(I)由已知椭圆C的离心率


从而椭圆的方程为
(II)设







则

即点M的坐标为
同理,设直线A2N的斜率为k2,则得点N的坐标为




又


故当
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列





(Ⅰ)对任意实数

(Ⅱ)试判断数列
(Ⅲ)设







正确答案
(Ⅰ)证明:假设存在一个实数λ,使{an}是等比数列,则有a22=a1a3,即

所以{an}不是等比数列.
(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3(n-1)+21]=(-1)n+1(
=

又b1x-(λ+18),所以
当λ=-18,bn=0(n∈N+),此时{bn}不是等比数列:
当λ≠-18时,b1=(λ+18) ≠0,由上可知bn≠0,∴
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,-
(Ⅲ)由(Ⅱ)知,当λ=-18,bn=0,Sn=0,不满足题目要求.
∴λ≠-18,故知bn= -(λ+18)·(-
Sn=-
要使a<Sn<b对任意正整数n成立,
即a<-


当n为正奇数时,1<f(n)
∴f(n)的最大值为f(1)=

于是,由①式得

当a<b

当b>3a存在实数λ,使得对任意正整数n,都有a<Sn<b,且λ的取值范围是(-b-18,-3a-18)。
解析
解析已在路上飞奔,马上就到!