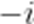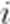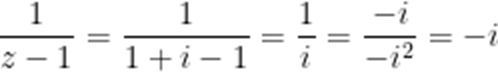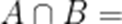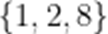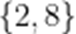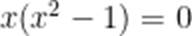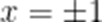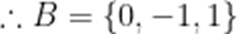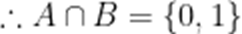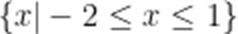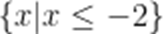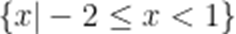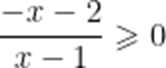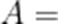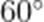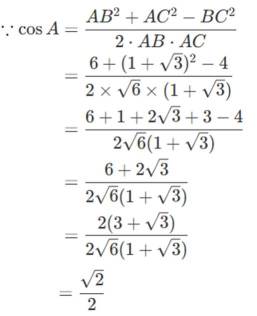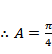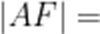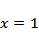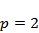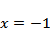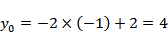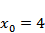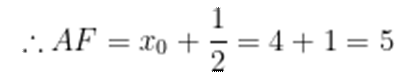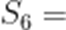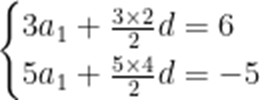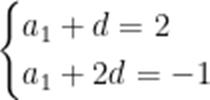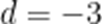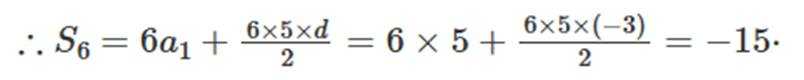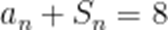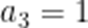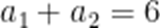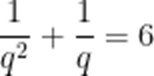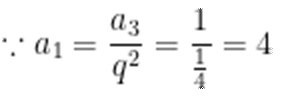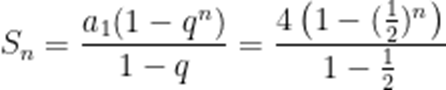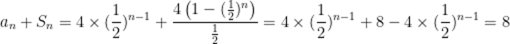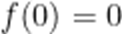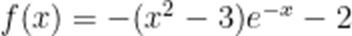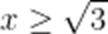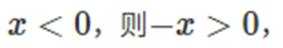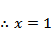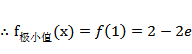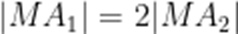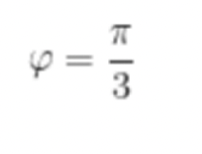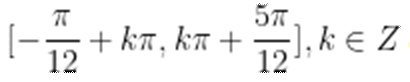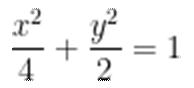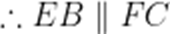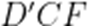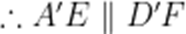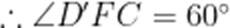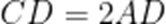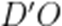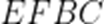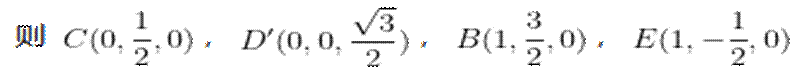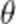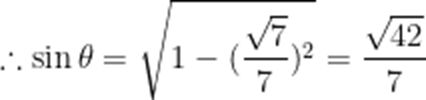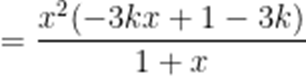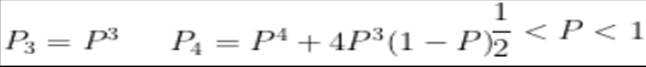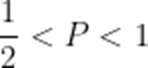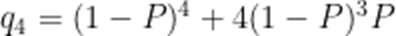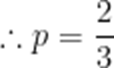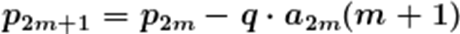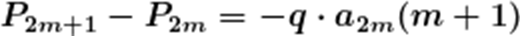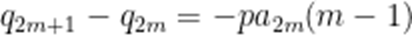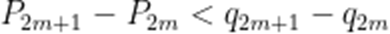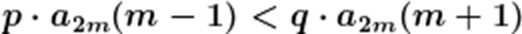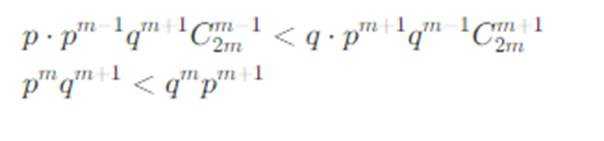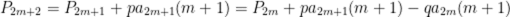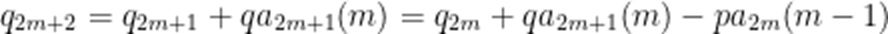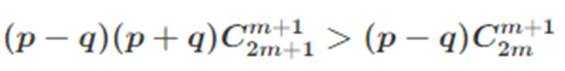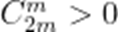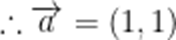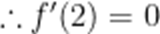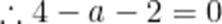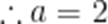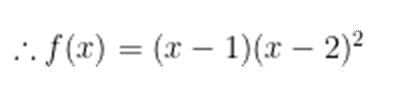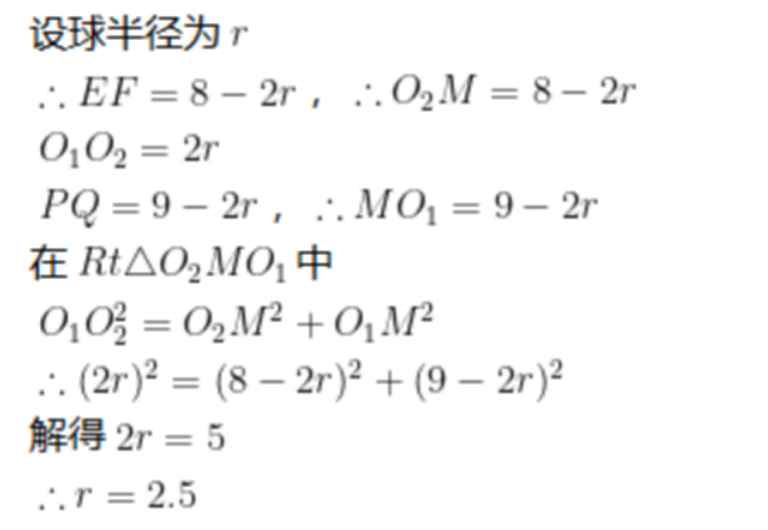样本数据2,8,14,16,20的平均数为
A.8
B.9
C.12
D.18
正确答案
C
解析
本题考查了样本平均数,考查运算能力
故答案为C
已知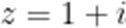
A.
B.
C.-1
D.1
正确答案
A
解析
本题考查了复数的运算
已知集合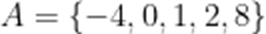
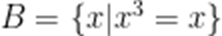
A.
B.
C.
D.
正确答案
D
解析
本题考查了集合的运算、交集、解方程
由 B: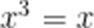

不等式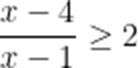
A.
B.
C.
D.
正确答案
C
解析
本题考查了解分式不等式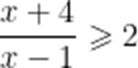
通分
等价转化为
解得:
在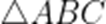


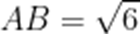
A.
B.
C.
D.
正确答案
A
解析
本题考查了余弦定理的应用
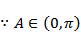
故选
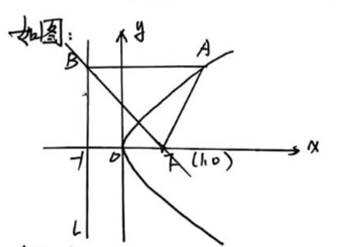
设抛物线C: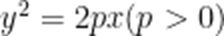
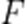


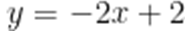
A.3
B.4
C.5
D.6
正确答案
C
解析
本题考查了抛物线的定义,考查了直线与抛物线的位置关系.
如图:
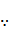
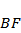
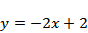


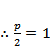

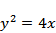

设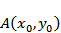
令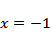
则
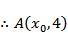

故选C.
记
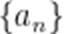
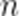
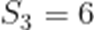
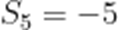
A.-20
B.-15
C.-10
D.-5
正确答案
B
解析
【解析】本题考查了等差数列的求和公式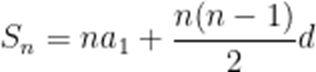
即
解得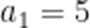
故选B
已知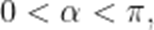
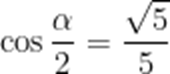
A.
B.
C.
D.
正确答案
D
解析
故选D
记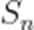
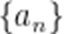
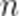
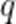

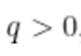

A.
B.
C.
D.
正确答案
AD
解析
本题考查了等比数列的通项公式、等比数列的求和公式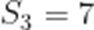
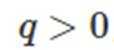
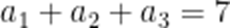
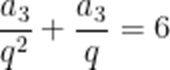
整理得
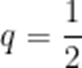

故A正确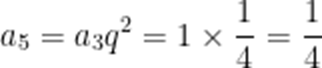
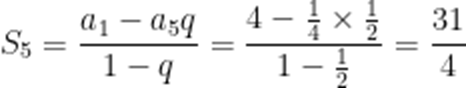
故D正确
已知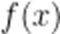

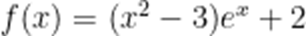
A.
B.当x<0时,
C.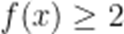
D.

正确答案
ABD
解析
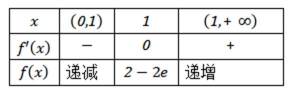
本题考查了函数的奇偶性、对称性,导数研究函数的单调性、极值
∵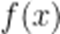
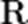
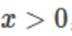
设
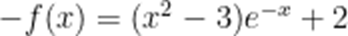
当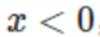
故B正确
由奇函数的性质,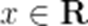
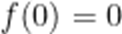
因为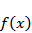
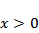
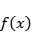
当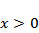
令
则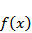
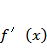
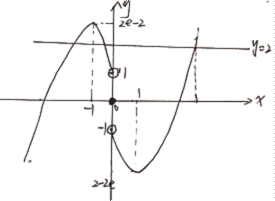
故由函数关于原点对称,其图像大致如下
故
由图像可知,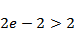
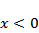
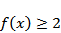

双曲线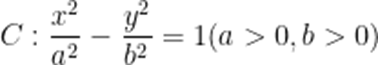
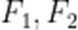
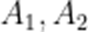
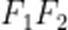

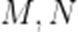

A.
B.
C.
D.当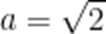

正确答案
ACD
解析
本题考查了双曲线的性质,双曲线的渐近线,考查了直线与圆相交,以及求双曲线的离心率.
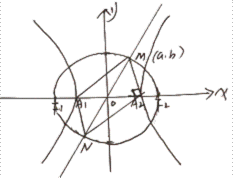
如图
双曲线的渐近线为
过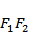
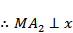

则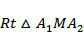
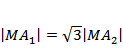
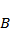
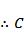
当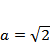
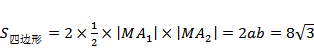
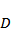
已知函数
(1)求
(2)设函数

正确答案
(1)
(2)g(x)的值域:
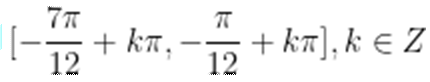
解析
本题考查了三角恒等变换、三角函数的值域和单调区间的求法
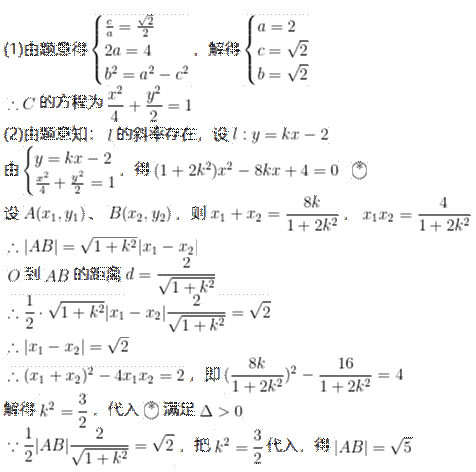
已知椭圆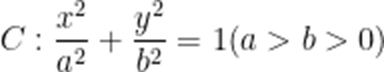

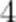
(1)求
(2)过点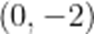

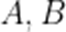


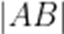
正确答案
(1)
(2)
解析
本题考查了椭圆标准方程的求法,直线与椭圆的位置关系、弦长公式等知识.
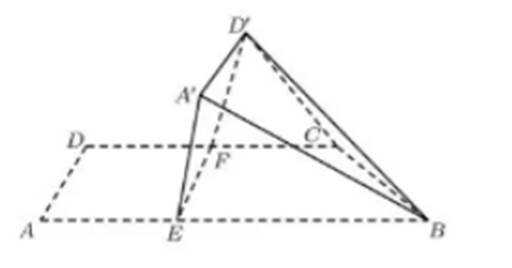
如图,四边形ABCD中,AB∥CD,∠DAB=90°,F为CD中点,E在AB上,EF∥AD,AB=3AD,CD=2AD.将四边形EFDA沿EF翻折至四边形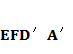
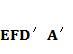
(1)证明:
(2)求面

正确答案
(1)见解析
(2)
解析
本题考查了线面平行的证明,及空间向量求二面角的知识.
(1) 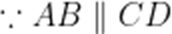
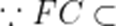
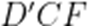

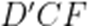
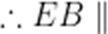
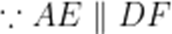
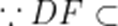
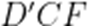
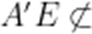
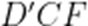
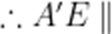
又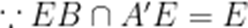
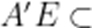
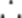
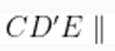



(2)由折叠关系知,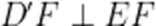
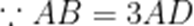
不妨设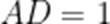
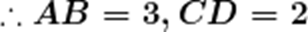
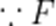
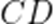
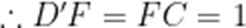
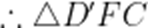
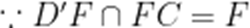
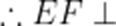
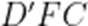


可知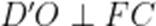
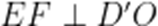
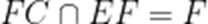
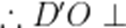


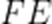

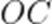
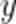

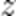
设平面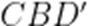
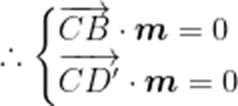
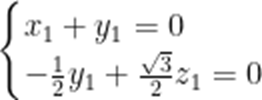

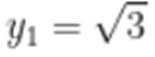
设平面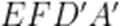
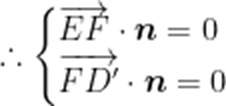
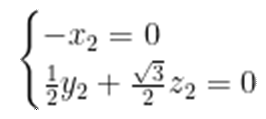
设平面
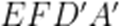

已知函数
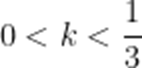
(1)证明:
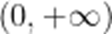
(2)设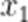
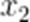
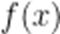
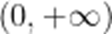
①设函数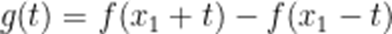
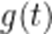
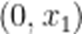
②比较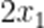
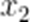
正确答案
(1)见解析
(2)①见解析
②
解析
本题主要考查了函数的极值点和零点,利用导数证明函数的单调性,及比较大小.
(1).
令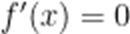
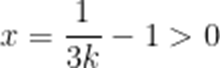
令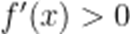
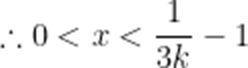
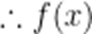
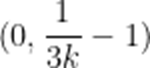
令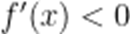

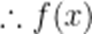
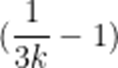
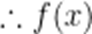

即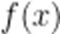
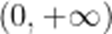
又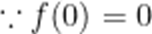
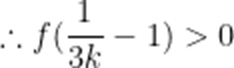
当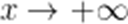



甲、乙两人进行乒乓球练习,每个球胜者得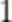
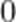
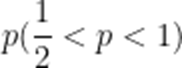
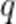

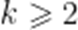
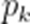
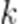
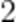
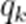

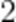
(1)求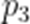
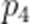
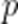
(2)若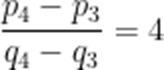
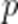
(3)证明:对任意正整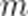
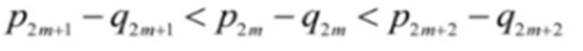
正确答案
(1)
(2)
(3)见解析
解析
(1) 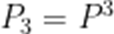
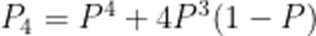
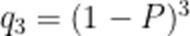
(2)
(3)记
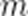
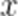
故
故要证:
只需证:
即只需证:
即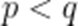
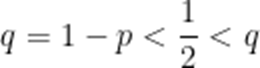
由
现在,考虑不等式右边 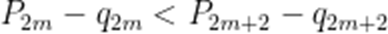
只需证
只需证:
只需证
只需证:
因为
故上面不等式成立,证毕.
已知平面向量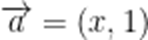
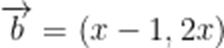


正确答案
解析
本题考查了向量的坐标运算和向量垂直的条件及向量的模.
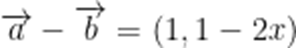
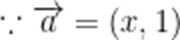
故答案为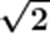
若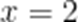
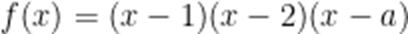

正确答案
-4
解析
本题考查了利用导数研究函数的极值,由极值点求参数的值.
故答案为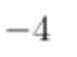
一个底面半径为
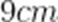

正确答案
2.5
解析
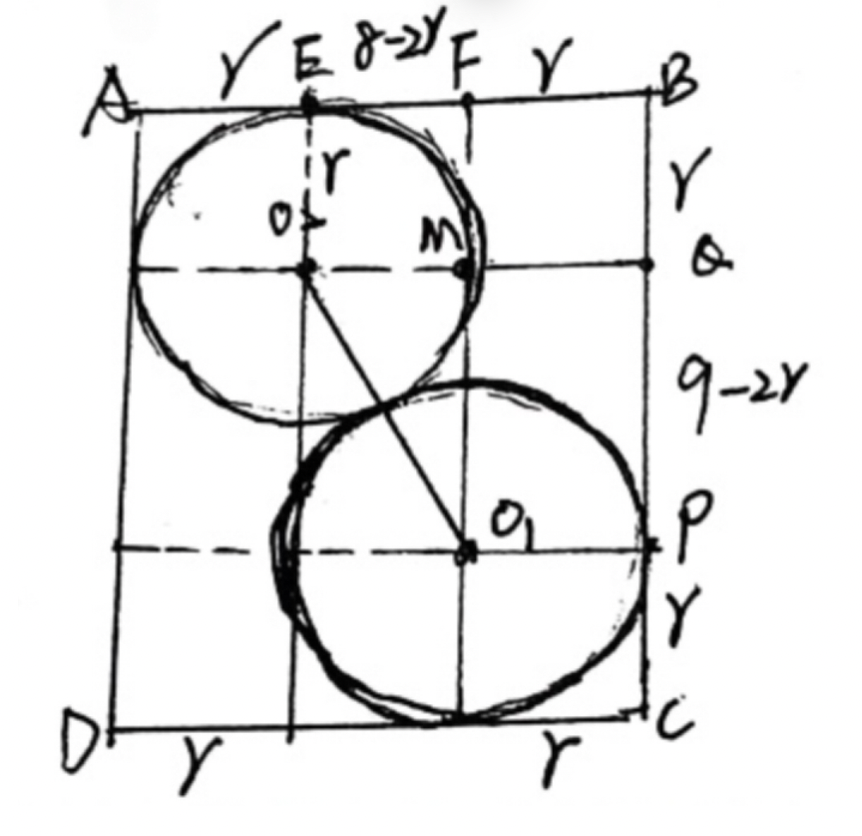
本题考查了立体几何中的球的切接问题.
如图:作出圆柱与球的轴截面
故答案为2.5