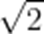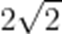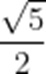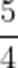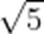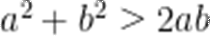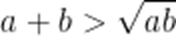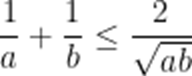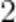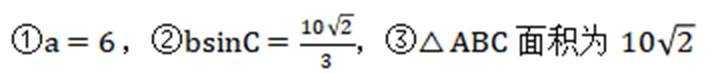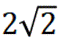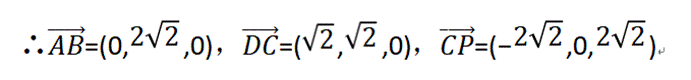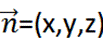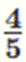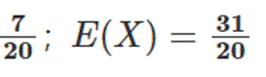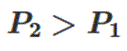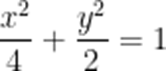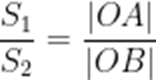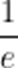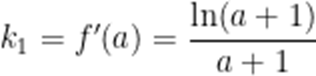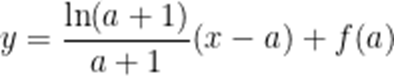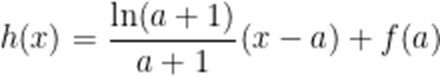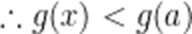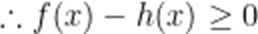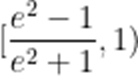(☆☆)集合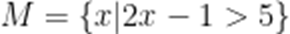
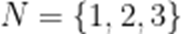
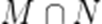
A.{1,2,3}
B.{2,3}
C.{3}
D.
正确答案
D
(☆☆)已知复数z满足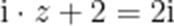
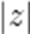
A.
B.
C.4
D.8
正确答案
B
(☆☆)双曲线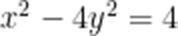
A.
B.
C.
D.
正确答案
B
(☆☆)为得到函数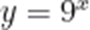
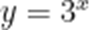
A.横坐标变成原来的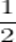
B.横坐标变成原来的2倍,纵坐标不变
C.纵坐标变成原来的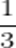
D.纵坐标变成原来的3倍,横坐标不变
正确答案
A
(☆☆)已知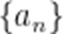
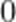
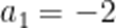

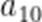
A.-20
B.-18
C.16
D.18
正确答案
C
(☆☆)已知a>0,b>0,则()
A.
B.
C.
D.
正确答案
C
(☆☆)已知函数f(x)的定义域为D,则“函数f(x)的值域为R”是“对任意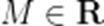
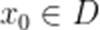
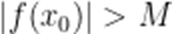
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
正确答案
A
(☆☆)设函数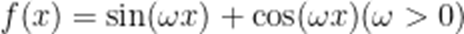
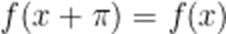
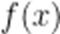
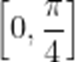
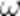
A.8
B.6
C.4
D.3
正确答案
C
(☆☆)在一定条件下,某人工智能大语言模型训练N个单位的数据量所需要时间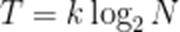
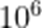
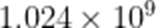
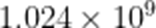
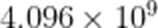
A.
B.
C.
D.
正确答案
B
(☆☆)已知平面直角坐标系xOy中,
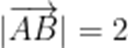
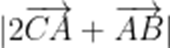
A.[6,14]
B.[6,12]
C.[8,14]
D.[8,12]
正确答案
D
(☆)已知抛物线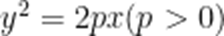
正确答案
6
(☆☆)已知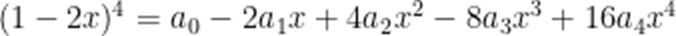
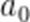
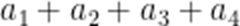
正确答案
①1
②15
(☆☆)已知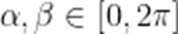
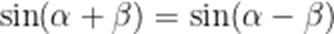
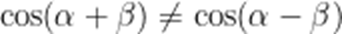
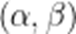
正确答案
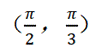
(☆☆)某科技兴趣小组使用3D打印机制作的一个零件可以抽象为如图所示的多面体,其中ABCDEF是一个平行多边形,平面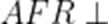
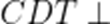
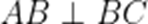
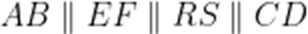
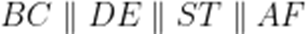

正确答案
60
(☆☆)关于定义域为R的函数f(x),以下说法正确的有.
①存在在R上单调递增的函数f(x)使得f(x)+f(2x)=-x恒成立;
②存在在R上单调递减的函数f(x)使得f(x)+f(2x)=-x恒成立;
③使得f(x)+f(-x)=cosx恒成立的函数f(x)存在且有无穷多个;
④使得f(x)-f(-x)=cosx恒成立的函数f(x)存在且有无穷多个.
正确答案
②③
在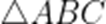
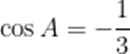
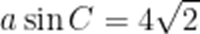
(1)求c;
(2)在以下三个条件中选择一个作为已知,使得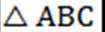
正确答案
(1)c=6
(2)选②,BC边上的高为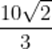
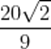
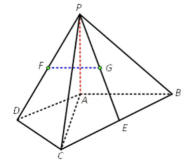
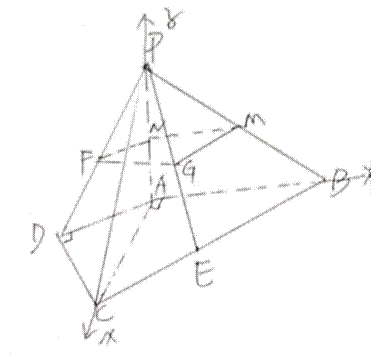
四棱锥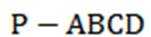
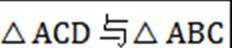
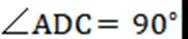
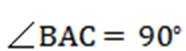
(1)F为PD的中点,G为PE的中点,证明:
(2)若
正确答案
(1)证明:取PA的中点N,PB的中点M,连接FN、MN
∵△ACD与△ABC为等腰直角三角形∠ADC=90∘,∠BAC=90∘
不妨设AD=CD=2,∴AC=AB=
∴BC=4,∵E、F分别为BC、PD的中点∴FN=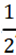
∴GM=1
∵∠DAC=45∘,∠ACB=45∘
∴AD∥BC,
∴FN∥GM
∴四边形FGMN为平行四边形
∴FG∥MN
∵FG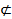
(2)∵PA⊥面ABCD,∴以A为原点,AC、AB、AP所在直线分别为x、y、z轴建立如图所示的空间直角坐标系,
设AD=CD=2,则A(0,0,0),B(0,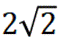
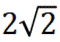
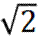
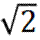
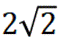
设面PCD的一个法向量为
有一道选择题考查了一个知识点,甲、乙两校各随机抽取100人,甲校有80人答对,乙校有75人答对,每位同学是否答对相互独立,用频率估计概率.
(1)从甲校随机抽取1人,求这个人做对该题目的概率;
(2)从甲、乙两校各随机抽取1人,设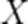
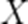
(3)若甲校同学掌握这个知识点,则有100%的概率做对该题目,乙校同学掌握这个知识点,则有85%的概率做对该题目,未掌握该知识点的同学都是从四个选项里面随机选择一个,设甲校学生掌握该知识点的概率为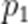
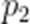
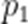
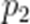
正确答案
(1)
(2)1人做对的概率
(3)
已知椭圆E: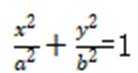
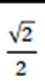
(1)求椭圆方程;
(2)设O为原点,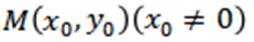
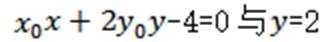


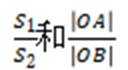
正确答案
(1)
(2)
函数f(x)定义域为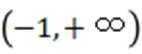
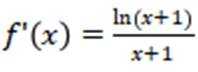
处的切线为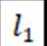
(1)求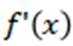
(2)证明:当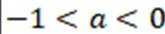
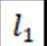
(3)当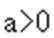
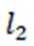
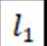
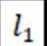
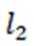
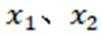
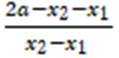
正确答案
(1)
(2) 设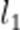
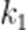
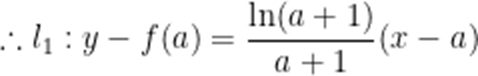
设
令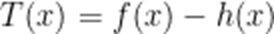
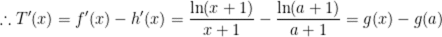
由(1)知,当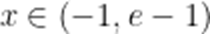
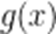
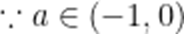
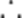
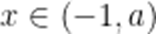
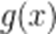
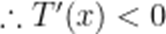
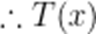
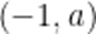
当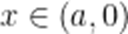
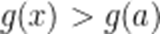
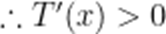
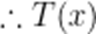
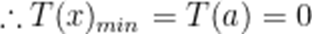
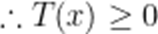
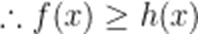
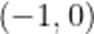
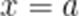
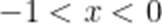
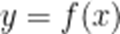
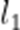
(3)
A={1,2,3,4,5,6,7,8},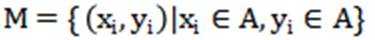
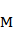

列: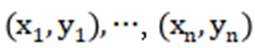
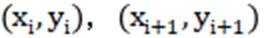
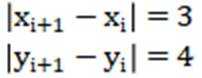
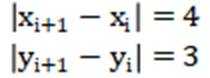
(1)若K列的第一项为(3,3),求第二项;
(2)若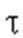
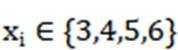
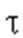
(3)证明:M中所有元素都不构成K列.
正确答案
(1)(6,7)或(7,6)
(2)不能
(3)由题知,M为点集,由(2)知,设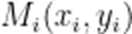
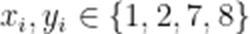
则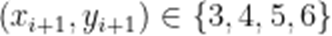
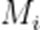
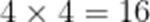
而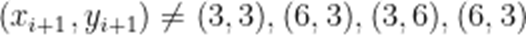
横、纵坐标不能同时相差4,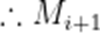
即对于16个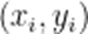
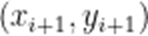
综上,M中所有元素都无法构成K列.