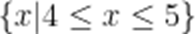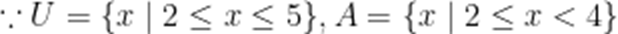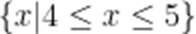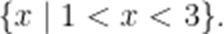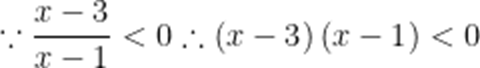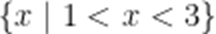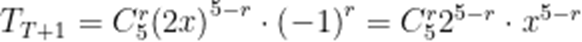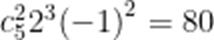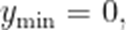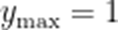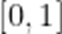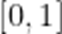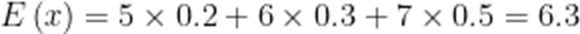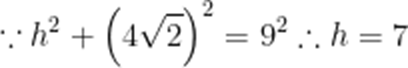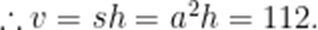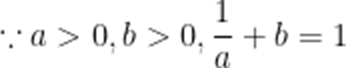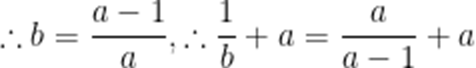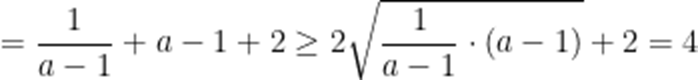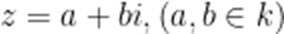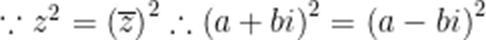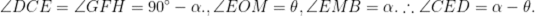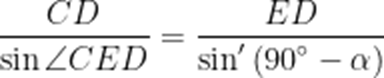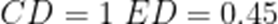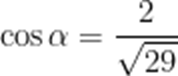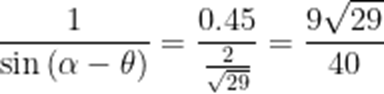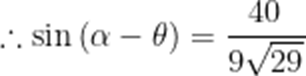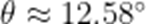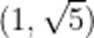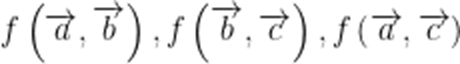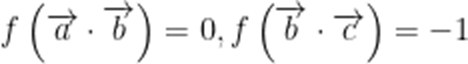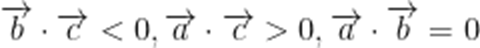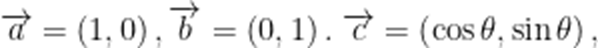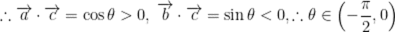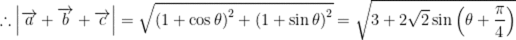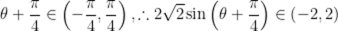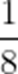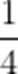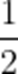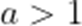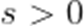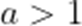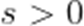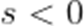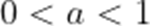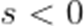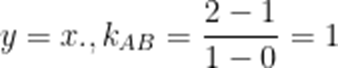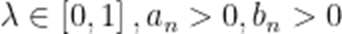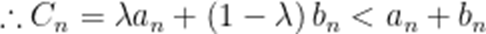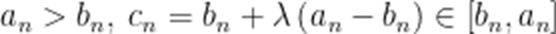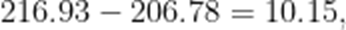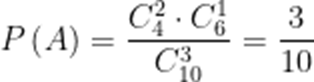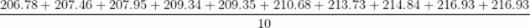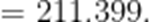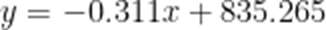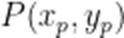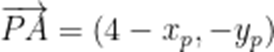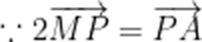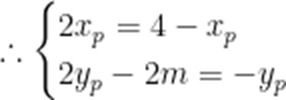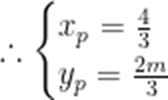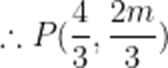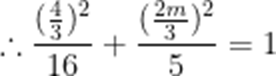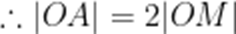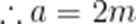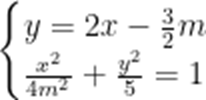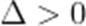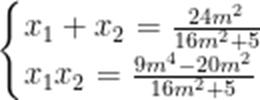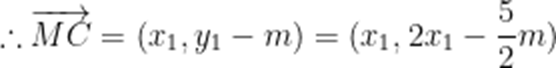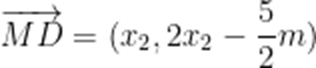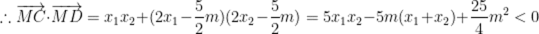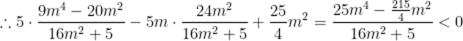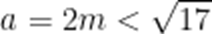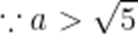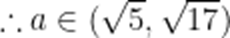已知全集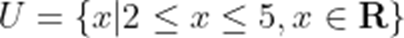
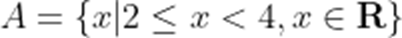
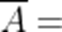
正确答案
解析
本题考查了补集的运算，：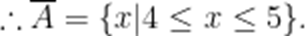
不等式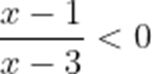
正确答案
解析
本题考查了分式不等的解法.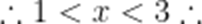
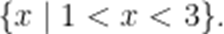
已知等差数列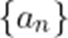
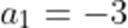
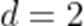
正确答案
12
解析
本题考查了等差数列的求和公式的应用.
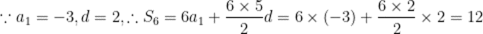
故答案为：12
在二项式
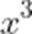
正确答案
80
解析
本题考查了二项式定理中项的系数的求法
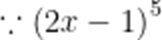
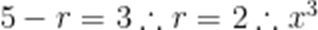
故答案为：80
函数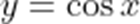
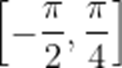
正确答案
[0,1]
解析
本题考查了余弦函数的值域
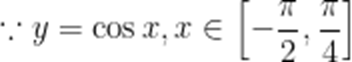
可知
当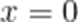
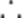
故答案为：
已知随机变量X的分布为
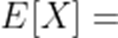
正确答案
6.3
解析
本题考查了离散型随机变量的数学期望
故答案为6.3
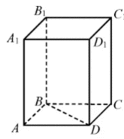
如图，在正四棱柱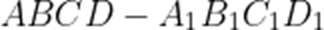
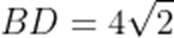
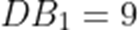
正确答案
112
解析
本题考查了柱体体积的水点
设底面边长为a,离为h,
则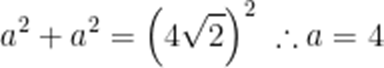
故答案为112.
设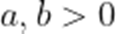
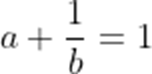
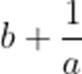
正确答案
4
解析
本题考查了利用基本不等式求最值
当且仅当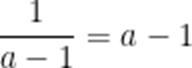
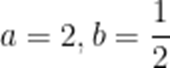
故答案为4.
4个家长和2个儿童去爬山.6个人需要排成一条队列，要求队列的头和尾均是家长，则不同的排列个数有______种.
正确答案
288
解析
本题考查了排列组合的应用
首先按排两个家长在两端,然后再排中间四次,共有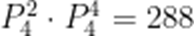
故答案为：288
已知复数z满足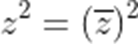
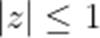
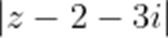
正确答案
解析
本题考差了复数的运算，复数的模的最值.
设
解得a=0或b=0，
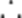
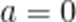
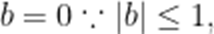
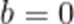
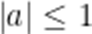
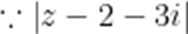
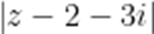
故答案：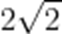
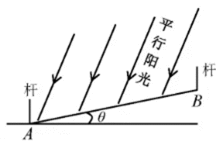
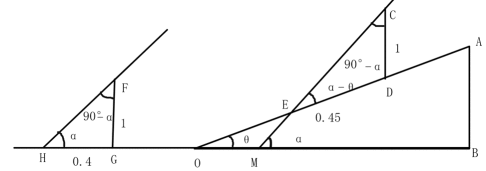
小申同学观察发现，生活中有些时候影子可以完全投射在斜面上．某斜面上有两根长为1米的垂直于水平面放置的杆子，与斜面的接触点分别为A、B，它们在阳光的照射下呈现出影子，阳光可视为平行光：其中一根杆子的影子在水平面上，长度为0.4米；另一根杆子的影子完全在斜面上，长度为0.45米．则斜面的底角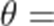
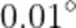
正确答案
12.58°
解析
本题考查了解三角形,正弦定理
如图
由题意可知.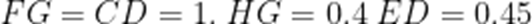
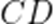
在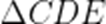
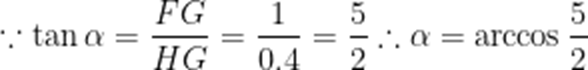
而
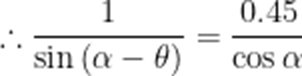
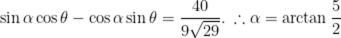
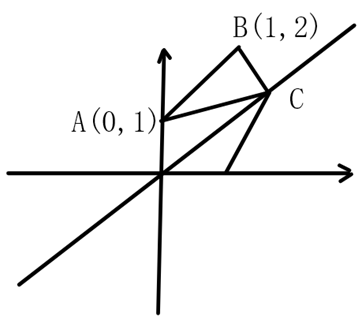
已知函数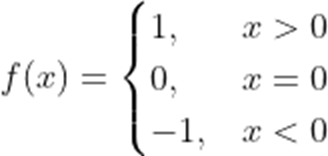
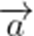
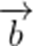
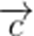
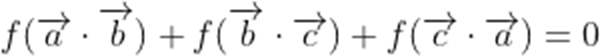
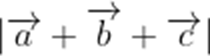
正确答案
解析
本是考查了平面向量的数量积,模的最值
由题意可知,
三者全为0或一个为1,一个为-1,一个为0。
当全为0时,可知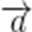
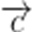
所以必为后者,不妨设
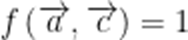
设
可知
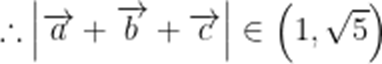
故答案为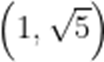
已知事件A、B相互独立，事件A发生的概率为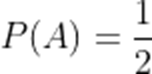
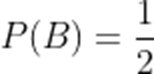
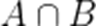
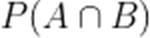
A
B
C
D0
正确答案
解析
本题考查相互独立事件的概率乘法公式
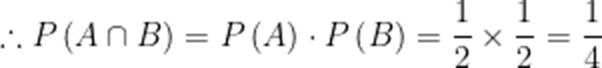
故选B.
设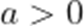
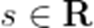
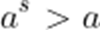
A
B
C
D
正确答案
解析
本题考差了指数函数的单调性.
由题意知,当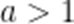
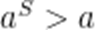
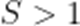
当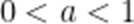
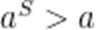
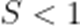
故选D.
已知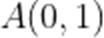
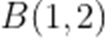
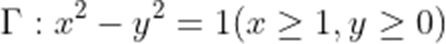
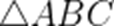
正确答案
解析
本题考查了双曲线的几何性质.
如图.
因为双曲线的渐近线方程为
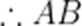
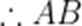
当C位于(1,0)时,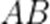
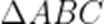
故选A.
设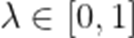
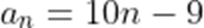
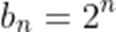
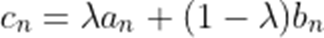
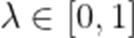
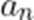
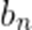
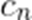
正确答案
解析
本题考查了数列的综合及分类讨论,转化思想
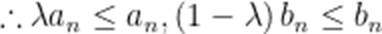
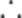
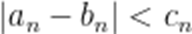
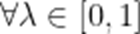
当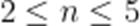
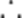
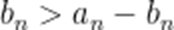
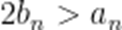
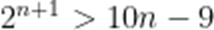
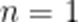
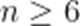
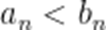
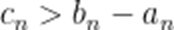
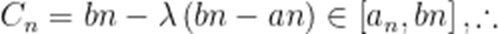
即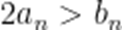
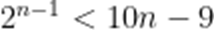
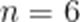
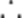
2024年东京奥运会，中国获得了男子4×100米混合泳接力金牌．以下是历届奥运会男子4×100米混合泳接力项目冠军成绩记录（单位：秒），数据按照升序排列．
206.78 207.46 207.95 209.34 209.35
210.68 213.73 214.84 216.93 216.93
(1)求这组数据的极差与中位数；
(2)从这10个数据中任选3个，求恰有2个数据在211以上的概率；
(3)若比赛成绩y关于年份x的回归方程为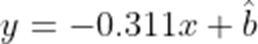
正确答案
（1）见解析（2）见解析（3）见解析
解析
本题考查了极差,中位数的求法、古典概率以及回归方程的应用.
(1)由题意,数据最大值为216.93,最小值为206.78,
故极差为
中位数为
(2)由题意,数据共有10个,211以上数据共有4个,
故设恰有2个211以上为事件A
所以,恰有2个数据在211以上的概率为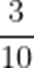
(3)由题意,比赛成绩y的平均权为
故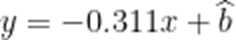
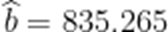
即
故要当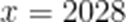
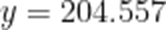
约为204.55
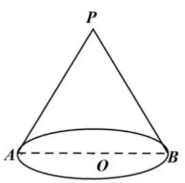
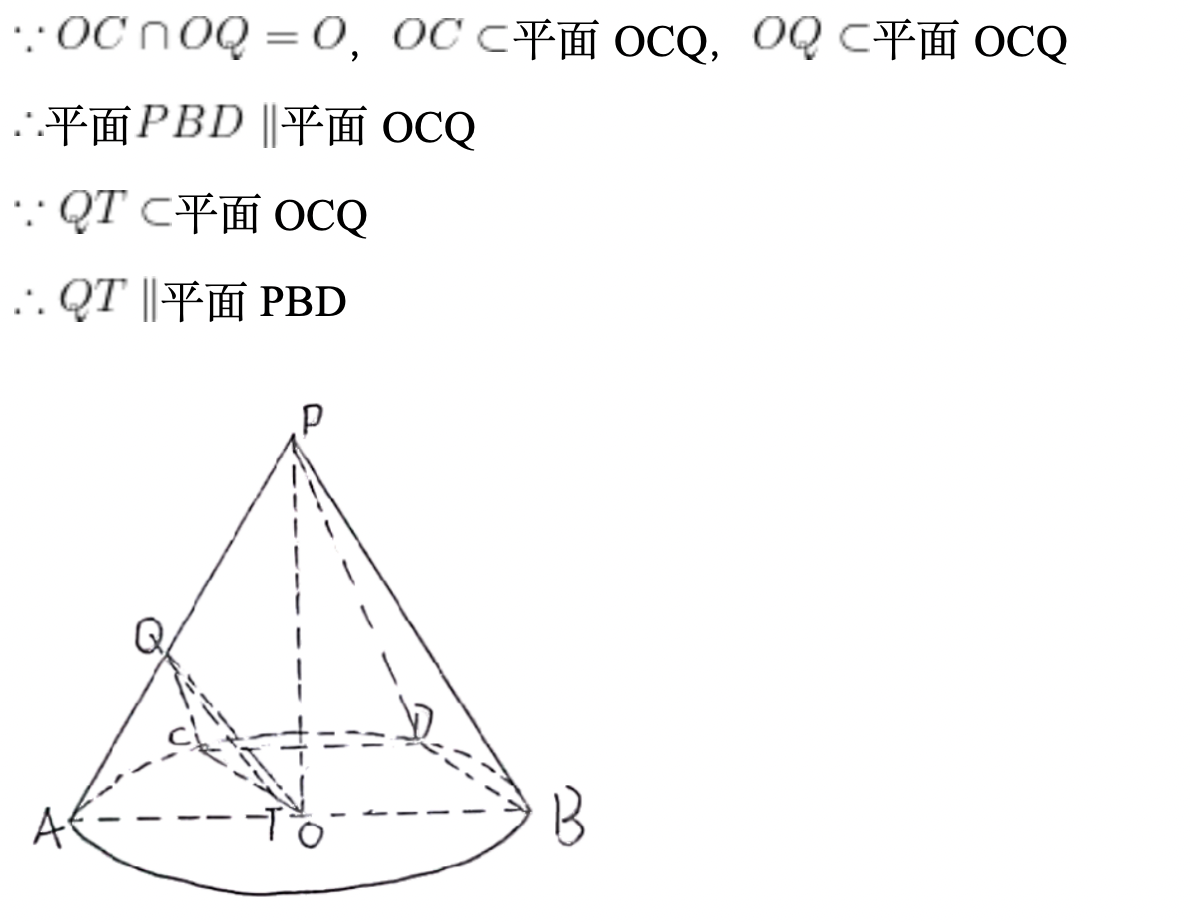
如图，P是圆锥的顶点，O是底面圆心，AB是底面直径，且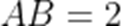
(1)若直线PA与圆锥底面的所成角为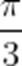
(2)已知Q是母线PA的中点，点C、D在底面圆周上，且弧
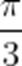
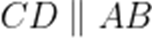
正确答案
（1）见解析（2）见解析
解析
本题考察了圆锥的面积、面面平行的判定与性质、线面平行的判定
(1)
(2)证明
已知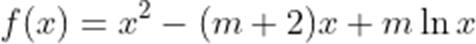
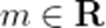
(1)若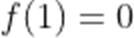
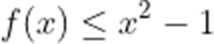
(2)若函数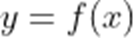
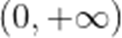
正确答案
（1）见解析（2）见解析
(1)由题意,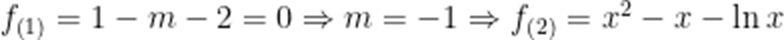
故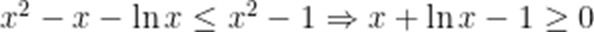
设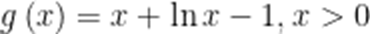
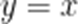
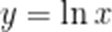
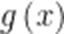
由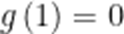
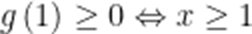
(2)由题意,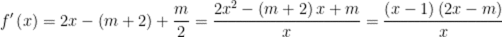
故分类讨论,由当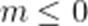
故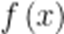
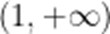
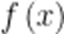
当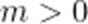
当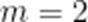
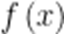
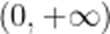
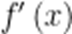
不成立；
当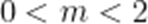
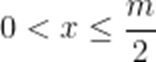
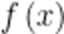
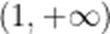
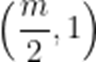
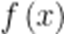
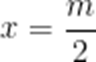
当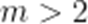
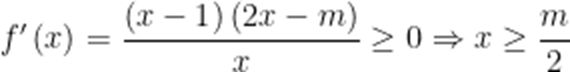
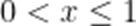
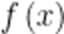
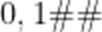
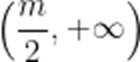
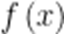
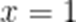
综上：
解析
本题考查了利用导数研究函数的单调性和极值,由极值求参数的取值范围,涉及到
分类讨论思想.
（第1小题满分4分，第2小题满分6分，第3小题满分8分）
已知椭圆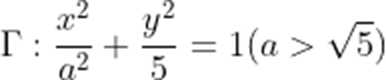
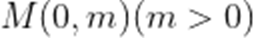
(1)若
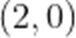
(2)若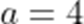
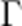
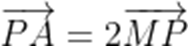
(3)若AM中垂线l的斜率为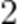
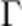
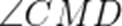
正确答案
（1）见解析（2）见解析（3）见解析
解析
本题考查了椭圆的离心率，直线与椭圆的位置关系，以及向量与椭圆的综合应用
(1)由题意，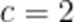
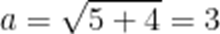
(2)由题意，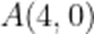
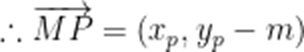
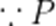
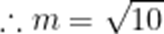
(3)由题意，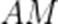
不防设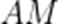
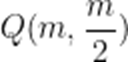
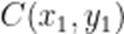
则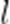
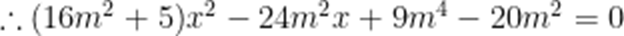
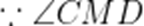
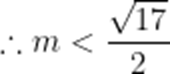
（第1小题满分4分，第2小题满分6分，第3小题满分8分）
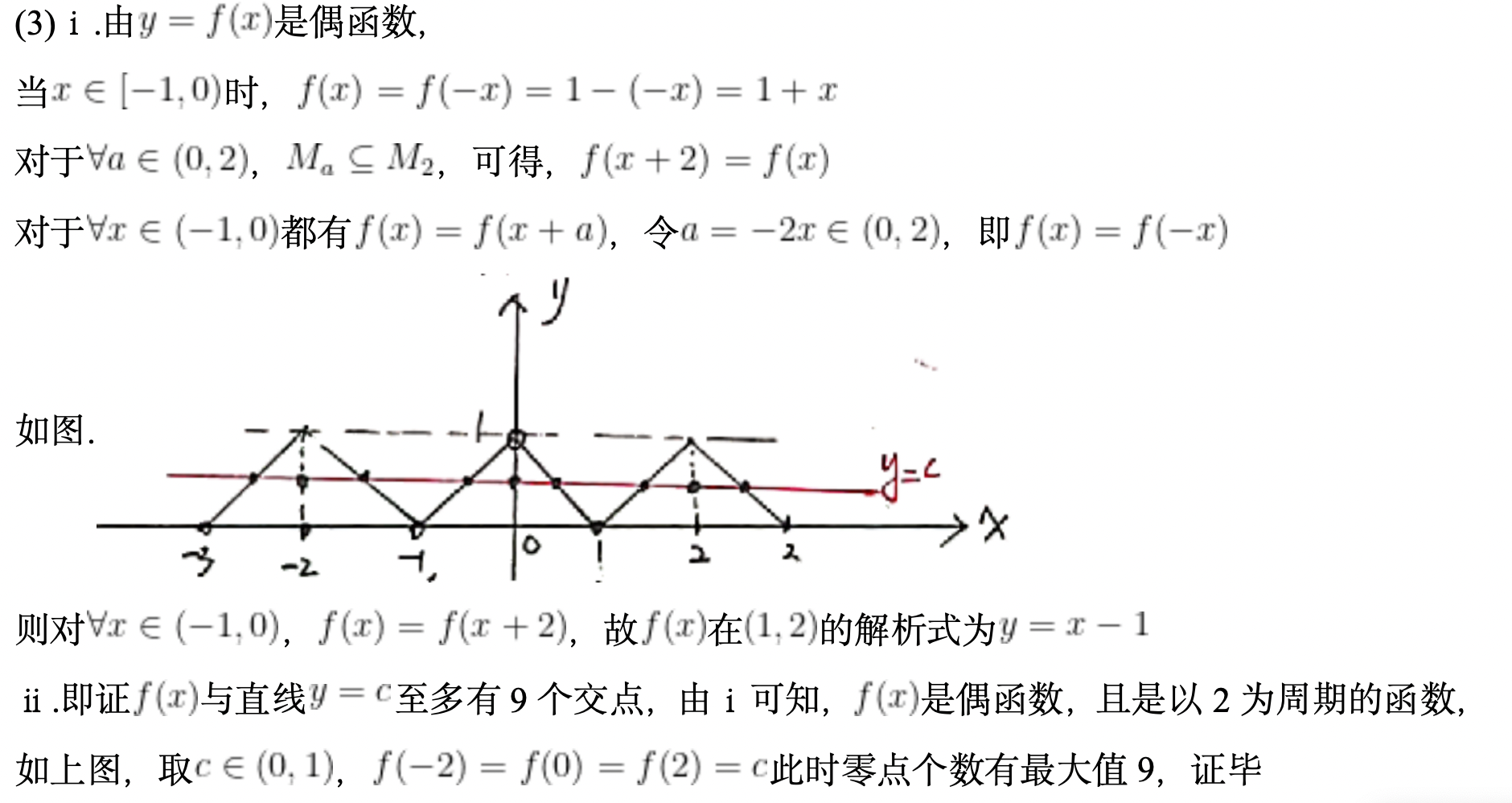
已知函数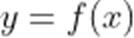
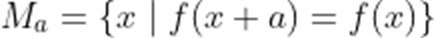
(1)若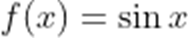
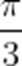
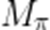
(2)若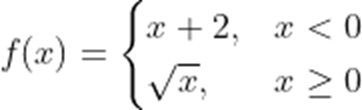
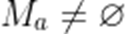
(3)设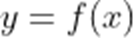
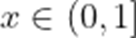
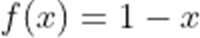
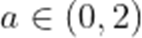
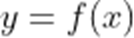
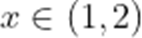
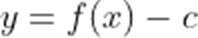
正确答案
（1）见解析（2）见解析（3）见解析
解析
本题考查了函数的新定义，函数的性质，奇偶性、周期性等，分类讨论、数形结合思想，函数的零点
(1)
(2)即存在x使得
在各自定义域上单调，故只可能是
(3)ⅰ.由
当
对于
对于
如图.
则对
ⅱ.即证
