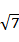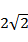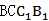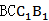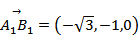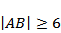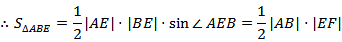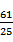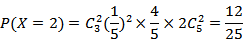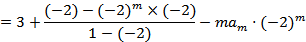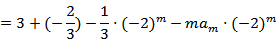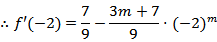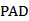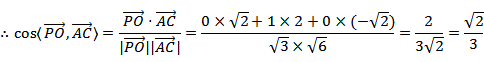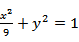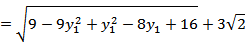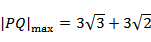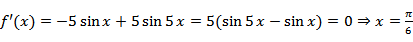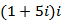
正确答案
解析
本题考查复数的运算及复数的概念.
由复数的乘法运算化简:

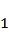
故选C.
设全集

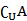
正确答案
解析
本题考查补集的运算及集合的列举法.
全集
又
则
故选C.
若双曲线


正确答案
解析
本题考查双曲线的离心率以及双曲线的实轴、虚轴
由题意


故选D.
已知点


正确答案
解析
本题考查正切函数的对称性.
由正切函数



由题意,


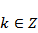


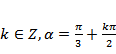
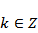


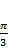
故选B.
设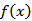




正确答案
解析
本题考查函数的周期性、奇偶性的应用.


又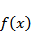
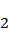
故选A.
帆船比赛中,运动员可借助风力计测定风速的大小和方向,测出的结果在航海学中称为视风风速,视风风速对应的向量,是真风风速对应的向量与船行风速对应的向量之和,其中船行风速对应的向量与船速对应的向量大小相等,方向相反。图1给出了部分风力等级、名称与风速大小的对应关系。已知某帆船运动员在某时刻测得的视风风速对应的向量与船速对应的向量如图2(风速的大小和向量的大小相同,单位m/s),则真风为( )
图1
图2
正确答案
解析
本题考查平面向量的坐标运算、向量的模的实际应用.
由题意视风风速=




故选A.
若圆

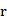
正确答案
解析
本题考查直线与圆位置关系的应用。
圆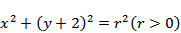
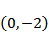

圆心







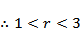
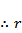

故选B.
若实数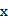

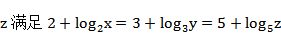



正确答案
解析
本题考查对数、指数的互化,排除法的应用.
设

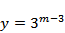

令



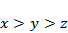
令




令
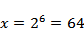


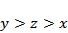
综上,本题选B.
在正三棱柱


正确答案
解析
本题考查线面垂直的判定,面面垂直的判定、性质,线面平行的判定,空间向量法判断线线平行或垂直,综合性较强.
设正三角形ABC的边长为2,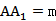
∵D为BC中点,∴AD⊥BC.
又

∴面ABC⊥面
又AD⊂面ABC,面ABC∩面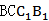
∴AD⊥面
取

选项A:


∴AD与
选项B:∵
∴
又AD⊥BC,


∴BC⊥面
选项C: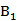



∴AD与
选项D:∵

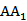





故选BD.
设抛物线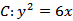








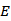
正确答案
解析
本题考查抛物线的几何性质,直线与抛物线的位置关系的应用.
选择题采用特殊位置,特殊值进行验证,比较迅速.
抛物线

选项A:由抛物线定义:得
选项B:设

联立
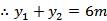
当m=0,即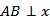
通径,

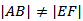
选项C:由B项得
选项D:直线AB:

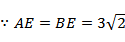
当

联立
即
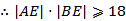
若直线
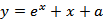
正确答案
4
解析
本题考查导数的几何意义:曲线在某点处的导数等于在该点处切线斜率.
由

设


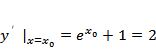

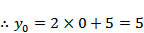
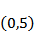




故答案为4.
若一个等比数列的前4项和为4,前8项和为68,则该等比数列的公比为______.
正确答案
解析
本题考查等比数列的通项公式:

由题意: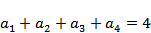


故答案为
一个箱子里有5个球,分别以1~5标号,若有放回取三次,记至少取出一次的球的个数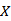

正确答案
解析
本题考查离散型随机变量的分布列以及期望.
由题意,至少取出一次的球的个数

为研究某疾病与超声波检查结果的关系,从做过超声波检查的人群中随机调查了1000人,得到如下的列联表:
(1)记超声波检查结果不正常者患该疾病的概率为

(2)根据小概率值
正确答案
(1)
(2)见解析.
解析
本题考查用频率估计概率、独立性检验.
(1)超声波检查结果不正常的有200人,其中患该疾病的有180人
由频率估计概率得:
(2)假设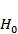
根据小概率值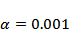

即认为超声波检查结果与是否患该病有关.
设数列

(1)证明:
(2)设

正确答案
(1)见解析.
(2)
解析
本题考查等差数列的判断,错位相减法求和以及导数的运算.
(1)构造出


(2)先对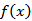

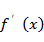

比”的形式,两边乘公比,由错位相减法求和.

求导得


①-②得:
如图所示的四棱锥

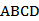
(1)证明:平面
(2)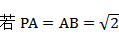







(i)证明:

(ii)求直线

正确答案
(1)见解析.
(2)(i)见解析.
(ii)直线AC与PO成角余弦值为
解析
本题考查面面垂直判定,性质,面面垂直的判定,空间向量求直线成角.
(1)证明:

又AB⊥AD,PA∩AD=A,PA、AD⊂面PAD.

又AB⊂面PAB

(2)




(i)设PBCD的外接球球心

①-④

(ii)由(i)得O在AD上且OA=1


已知椭圆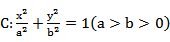


删除

(1)求C的方程;
(2)已知动点P不在y轴上,点

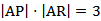
(i)设点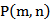



(ii)设O为坐标原点,Q是C上的动点,直线OQ的斜率是直线OP的斜率的3倍,求
正确答案
(1)椭圆
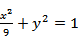
(2)(i)点R的坐标:
(ii)
解析
(1)椭圆

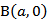


又椭圆离心率





(2)(i)设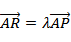

(ii)
整理得
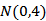
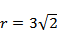
又点Q在椭圆



(1)求函数

(2)给定
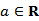


(3)设



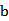
正确答案
(1)
(2)见解析
(3)
解析
(1)
当


当



(2)不妨设


若

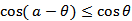

(3)方法二:由余弦函数周期性可令
当

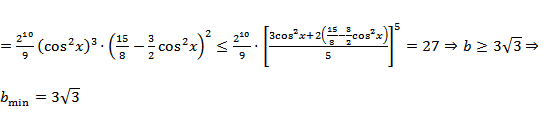
当

则
综上可得: