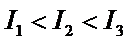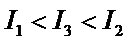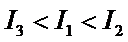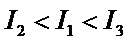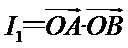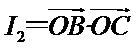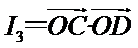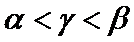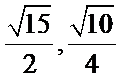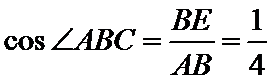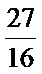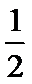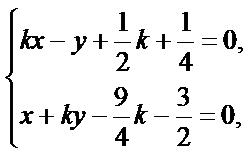6.已知等差数列{an}的公差为d,前n项和为Sn,则“d>0”是“S4 + S6>2S5”的( )
正确答案
解析

考查方向
解题思路
等差数列中
易错点
充要条件的判断
1.已知集合


正确答案
解析
取

考查方向
解题思路
直接利用并集定义进行计算即可
易错点
并集定义的合理运用
2.椭圆
正确答案
解析

考查方向
解题思路
由椭圆定义直接求出
易错点
椭圆中的
3.某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
正确答案
解析

考查方向
解题思路
几何体是三棱锥与半圆锥的组合体,根据三视图判断三棱锥的高及底面三角形的相关几何量的数据,判断半圆锥的高及底面半径,把数据代入三棱锥与半圆锥的体积公式计算可得.
易错点
根据三视图判断几何体的形状及数据所对应的几何量
4.若


正确答案
解析
可行域为一开放区域,直线过点
考查方向
解题思路
作出不等式组对应的平面区域,根据z的几何意义,利用数形结合即可得到结论.
易错点
z的几何意义
5.若函数f(x)=x2+ ax+b在区间[0,1]上的最大值是M,最小值是m,则M – m ( )
正确答案
解析
因为最值在

考查方向
解题思路
由二次函数在受限区间内在
易错点
受限区间二次函数最值
7.函数y=f(x)的导函数
正确答案
解析
原函数先减再增,再减再增,且
考查方向
解题思路
由导函数图象,知原函数先减再增,再减再增,且
易错点
函数的图象的判别
8.已知随机变量



正确答案
解析
∵


∴
考查方向
解题思路
已知随机变量服从两点分布,由两点分布知期望与方差,由0<p1<p2<

易错点
随机变量两点分布
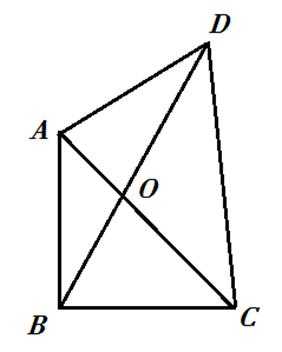
10.如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记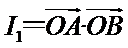
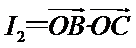
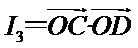
正确答案
解析
因为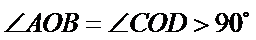
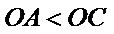
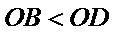
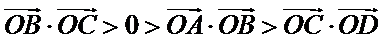
故选C.
考查方向
解题思路
由题知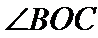
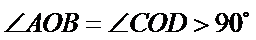
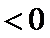
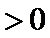
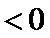
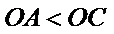
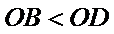
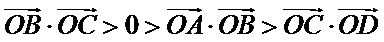
易错点
两个平面向量的夹角
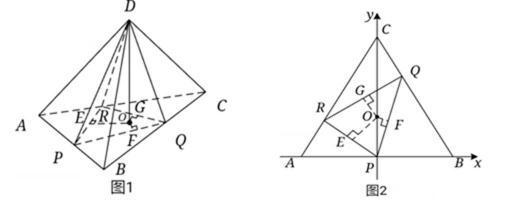
9.如图,已知正四面体D–ABC(所有棱长均相等的三棱锥),P,Q,R分别为AB,BC,CA上的点,AP=PB,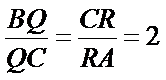
正确答案
解析
设O为三角形ABC中心,则O到PQ距离最小,O到PR距离最大,O到RQ距离居中,而高相等,因此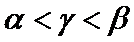
考查方向
解题思路
过点D作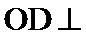
11.我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年.“割圆术”的第一步是计算单位圆内接正六边形的面积

正确答案
解析
将正六边形分割为6个等边三角形,则
考查方向
解题思路
单位圆内接正六边形,再将正六边形分割为6个等边三角形,所以6个正三角形的面积为正六边形的面积.
易错点
正六边形的边的关系
12.已知a,b∈R,

正确答案
5,2
解析
由题意可得



考查方向
解题思路
由


易错点
复数的四则运算
14.已知△ABC,AB=AC=4,BC=2. 点D为AB延长线上一点,BD=2,连结CD,则△BDC的面积是______,cos∠BDC=_______.
正确答案
解析
取BC中点E,DC中点F,由题意: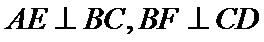
△ABE中,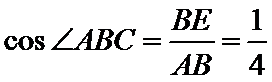
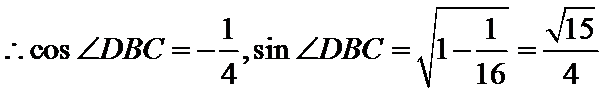
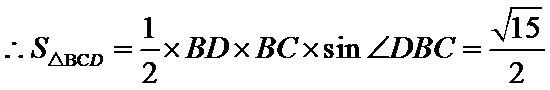
又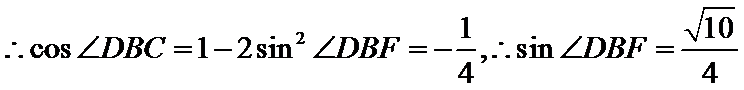
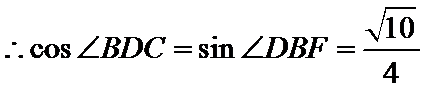
综上可得,△BCD面积为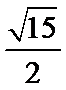
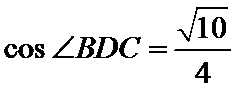
考查方向
解题思路
△ABE中,由余弦定理算出
易错点
正余弦定理的灵活运用
13.已知多项式


正确答案
16,4
解析
由二项式展开式可得通项公式为:





考查方向
解题思路
易错点
无
15.已知向量a,b满足

正确答案
4,
解析
设向量




令

据此可得:
即

考查方向
解题思路
设向量





易错点


16.从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有______种不同的选法.(用数字作答)
正确答案
660
解析
由题意可得:总的选择方法为: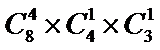
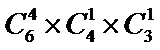
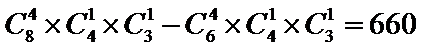
考查方向
解题思路
由题意直接算出总的选择方法,再算出不满足题意的选法,两者直接作差求出结果.
易错点
排列与组合的灵活运用
17.已知a


正确答案
解析

①当

函数的最大值
②当

③当




综上可得,实数

考查方向
解题思路
由



易错点
分类讨论的运用
18.(本题满分14分)已知函数f(x)=sin2x–cos2x–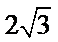
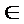
(Ⅰ)求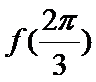
(Ⅱ)求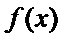
正确答案
(Ⅰ)2;(Ⅱ)最小正周期为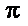
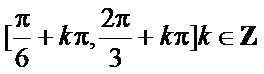
解析
(Ⅰ)由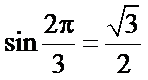
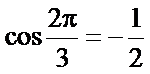
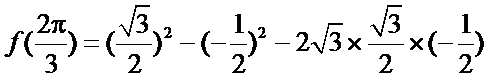
得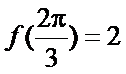
(Ⅱ)由题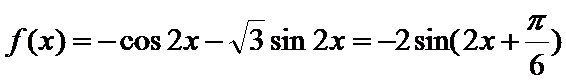
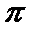
由正弦函数的性质得
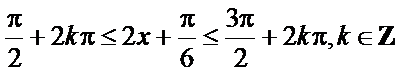
解得
所以,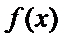
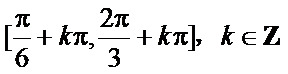
考查方向
解题思路
(I)直接将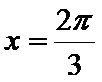
易错点
正弦型函数的性质应用
19.(本题满分15分)如图,已知四棱锥P–ABCD,△PAD是以AD为斜边的等腰直角三角形,
(Ⅰ)证明:
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
正确答案
(Ⅰ)见解析;(Ⅱ)
解析
(I)取PA的中点F,连接EF,CE
∵E为PD的中点,
∴EF∥AD
在四边形ABCD中,BC∥AD,AD=2DC=2CB,F为中点
易得EF∥CB,且EF=BC,
∴BCEF为平行四边形,
∴CE//BF
∵
而BF
∴EC∥平面PAB
(I)过P作PH⊥CD,交CD的延长线于点H
在Rt△PDH中,设DH=x,则易知
解得DH=



由题易得B(






则

设平面PBC的法向量为



设直线CE与平面PBC所成的角为θ,
则sinθ=
故直线CE与平面PBC所成角的正弦值为
考查方向
解题思路
(I)取AD的中点F,∴EF∥AD,又由AD=2DC=2CB,F为中点,易得EF∥CB,且EF=BC,∴BCEF为平行四边形,∴CE//BF即可证明结论;(II)过P作底面的垂线且与底面交于点O,以O为原点,OB所在直线为


易错点
(1)直线与平面平行的判断;(2)寻找法向量
20.(本题满分15分)已知函数f(x)=(x–


(Ⅰ)求f(x)的导函数;
(Ⅱ)求f(x)在区间
正确答案
(Ⅰ)

解析
(Ⅰ)因为

所以

(Ⅱ)由

解得


因为
又
所以f(x)在区间

考查方向
解题思路
(Ⅰ)直接根据函数的求导原则求导即可;(II)根所(Ⅰ)中求出导函数的正负得到函数的单调性及极值点,计算端点和极值,并证明
易错点
导函数的正负得出
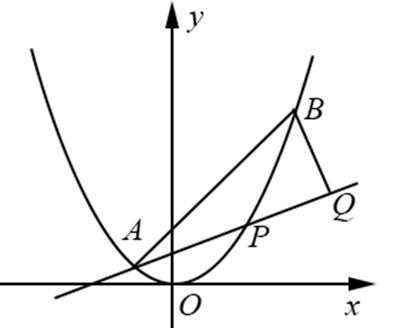
21.(本题满分15分)如图,已知抛物线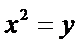
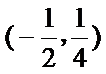
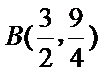
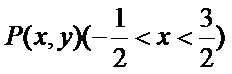
(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求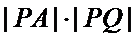
正确答案
(Ⅰ)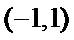
解析
(Ⅰ)由题易得P(x,x2),-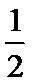
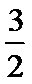
故kAP=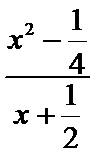
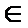
故直线AP斜率的取值范围为(-1,1).
(Ⅱ)联立直线AP与BQ的方程
解得点Q的横坐标是
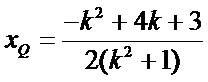
因为
|PA|=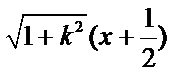
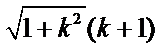
|PQ|= 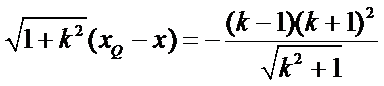
所以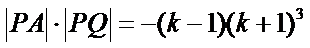
令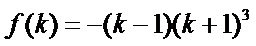
因为
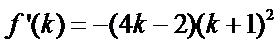
所以 f(k)在区间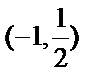
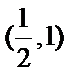
因此当k=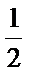
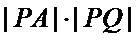
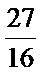
考查方向
解题思路
(I)由点P(x,x2),-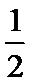
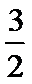
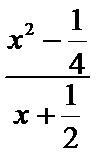
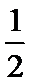
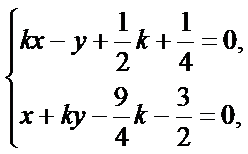
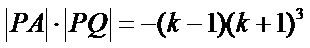
易错点
用导数研究函数的单调性
22.(本题满分15分)已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(
证明:当
(Ⅰ)0<xn+1<xn;
(Ⅱ)2xn+1− xn≤
(Ⅲ)

正确答案
(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)见解析.
解析
(Ⅰ)证明:令函数


又


又由

由
所以
(Ⅱ)由
记函数
函数

因此
(Ⅲ)
即

由

又由

即
综上可知,
考查方向
解题思路
(I)将数列和函数结合起来,








易错点
构造函数的灵活运用