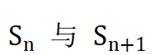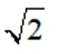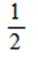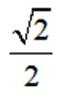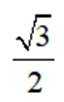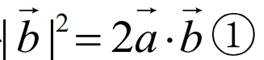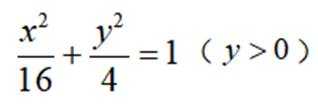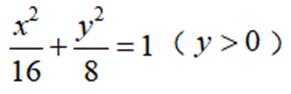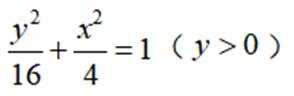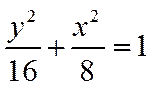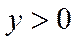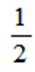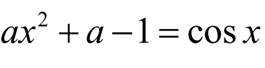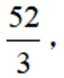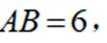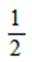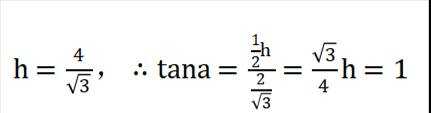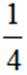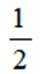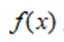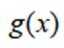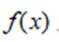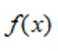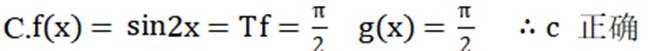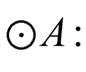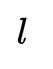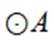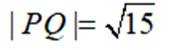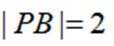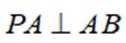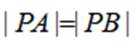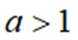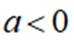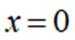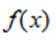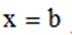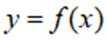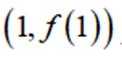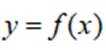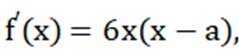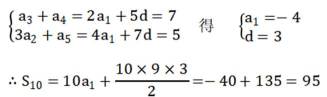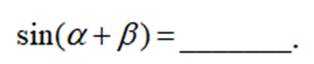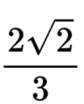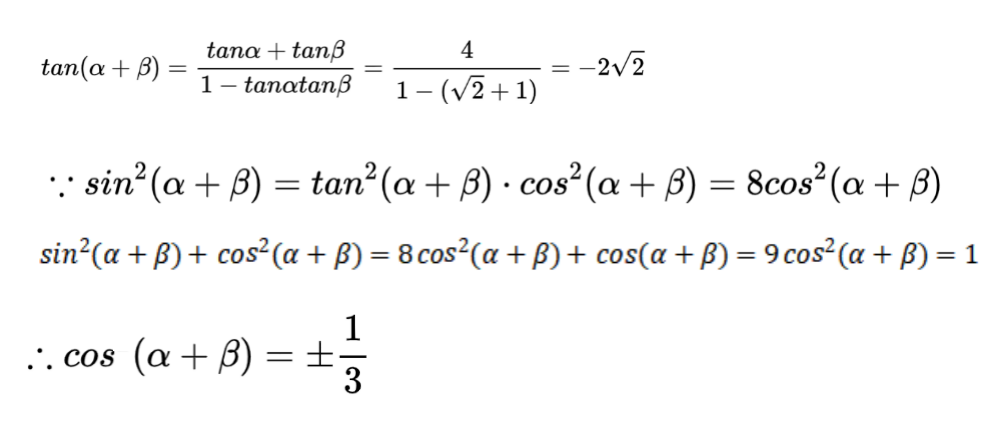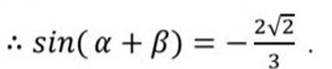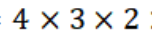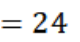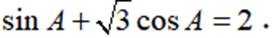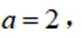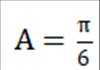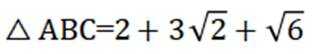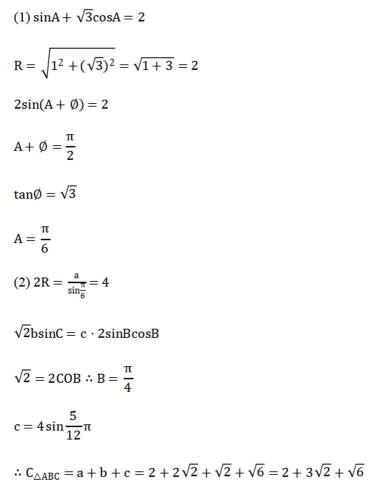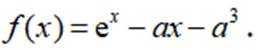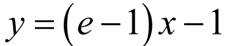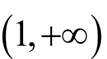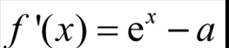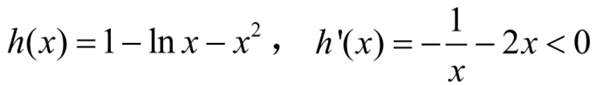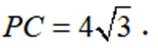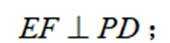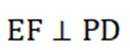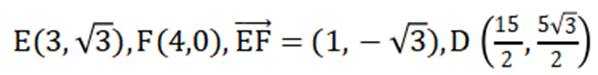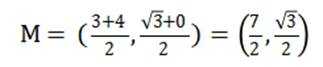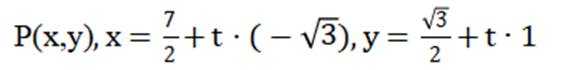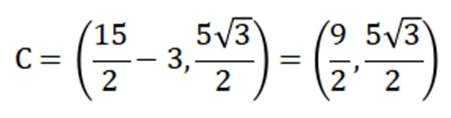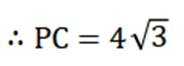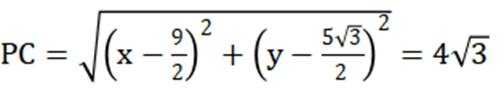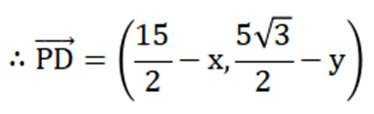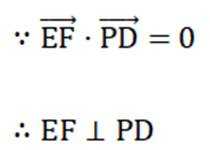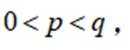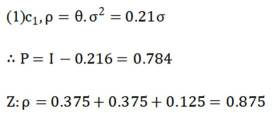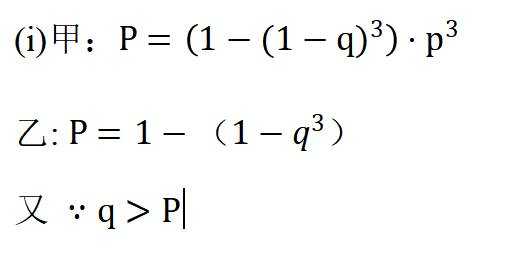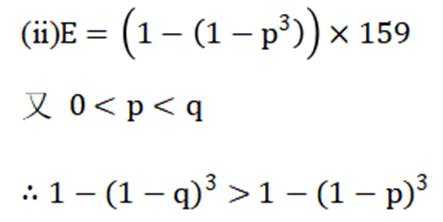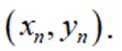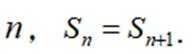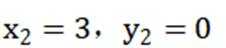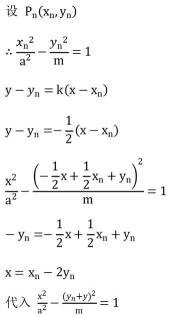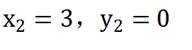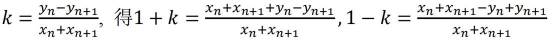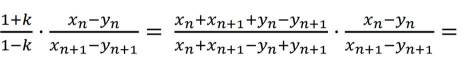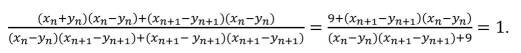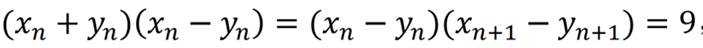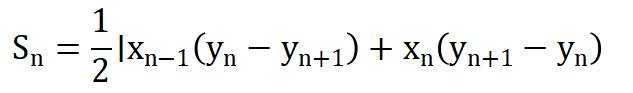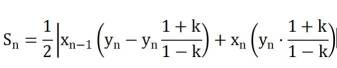已知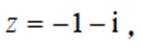
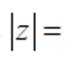
正确答案
解析
本题主要考查了复数的模的计算。
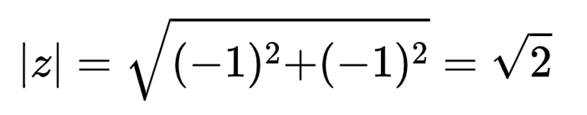
已知命题p: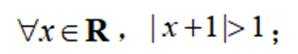

正确答案
解析
本题主要考查了命题的真假判断以及绝对值不等式、方程的求解等知识点。
p:当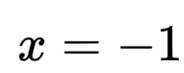

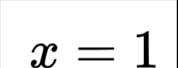
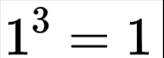
已知向量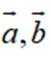
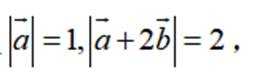
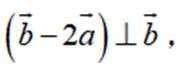
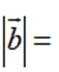
正确答案
解析
本题主要考查了向量的模、数量积以及垂直的相关知识点。
因为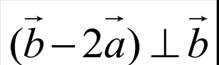
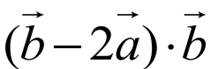
由题干知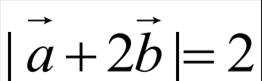
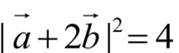
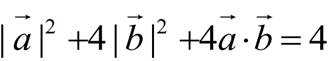
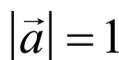
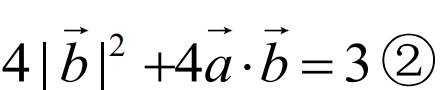
联立
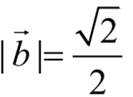
某农业研究部门在面积相等的100块稻田上种植一种新型水稻,得到各块稻田的亩产量(均在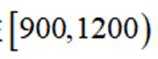
据表中数据,结论中正确的是( )
正确答案
解析
本题主要考查了中位数、频数、比例、极差以及平均值这些知识点。
根据频数分布表可知,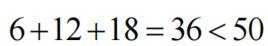
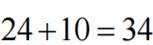


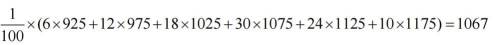
已知曲线C: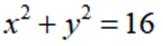
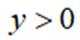
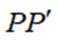
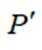
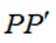
正确答案
解析
本题主要考查了曲线的轨迹方程以及坐标变换等知识点。
设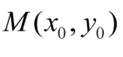
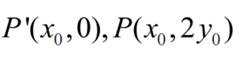
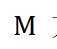
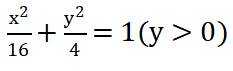
设函数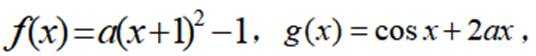

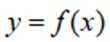
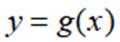
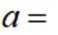
正确答案
解析
本题主要考查了函数的性质、方程的根以及导数的应用等知识点。
联立 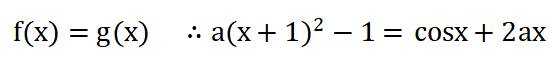
设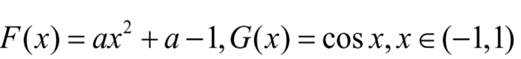
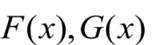
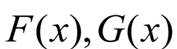
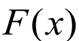
当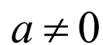

当
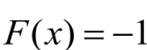
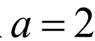
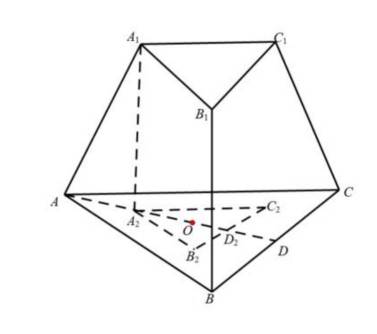
已知正三棱台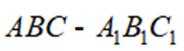
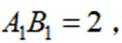
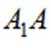
正确答案
解析
本题主要考查了正三棱台的体积公式,以及线面角的相关知识。
设高为 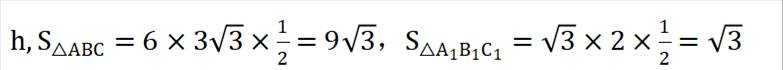
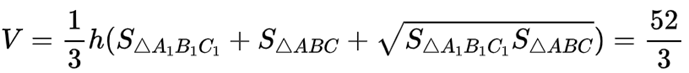
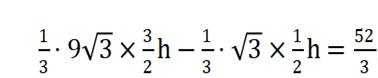
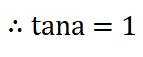
设函数
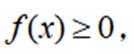
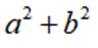
正确答案
解析
本题主要考查了函数的性质、不等式以及最值问题等知识点。
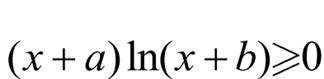
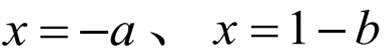
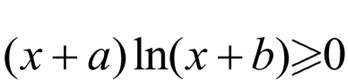
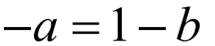
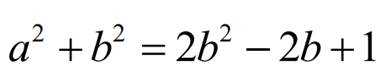
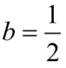
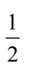
对于函数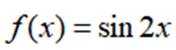
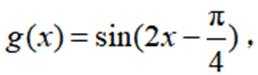
正确答案
解析
本题主要考查了三角函数的零点、最值、周期以及对称轴等知识点。
选项A.令
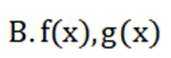
选项
选项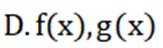
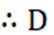
抛物线C: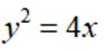
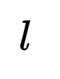
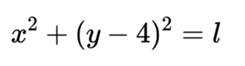
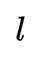
正确答案
解析
本题主要考查了抛物线的性质(如准线方程)、圆的切线性质、点到直线的距离公式、向量的数量积以及抛物线轨迹方程等知识点。
点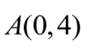
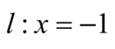
当P,A,B三点共线时,此时点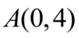
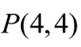
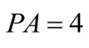
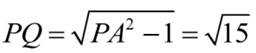
当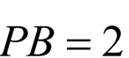
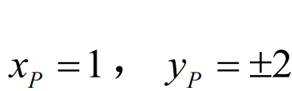
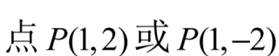
B为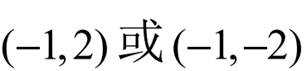

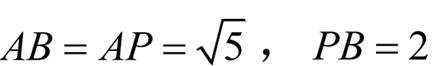
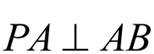
设抛物线的焦点为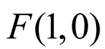
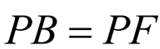
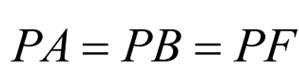

设函数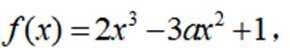
正确答案
解析
本题主要考查了函数的导数、极值、零点、对称轴以及对称中心等知识点。
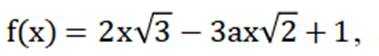
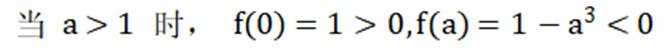
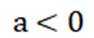
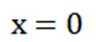
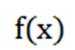
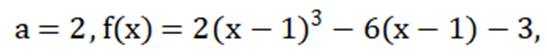
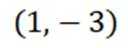
故选AD
记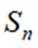

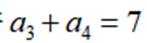
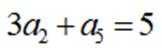
正确答案
95
解析
本题主要考查了等差数列的通项公式、等差数列的性质以及等差数列前n项和公式等知识点。
已知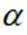

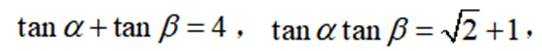
正确答案
_
解析
本题主要考查了三角函数的相关知识点。
在如图的4×4方格表中选4个方格,要求每行和每列均恰有一个方格被选中,则共有________种选法,在所有符合上述要求的选法中,选中方格中的4个数之和的最大值是________.
正确答案
24,112
解析
本题主要考查了排列组合的知识点。
(1)
(2)每列十位数字一样,故只要看个位,可选出15,21,33,43和最大: 15+21+33+43=112
记
(1)求A.
(2)若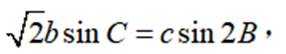
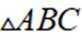
正确答案
(1)
(2)
解析
本题主要考查了辅助角公式、二倍角公式、正弦定理等知识点。
已知函数
(1)当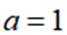
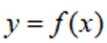
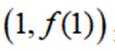
(2)若
正确答案
(1)
(2)
解析
本题主要考查了导数的计算与应用,包括求函数的导数,利用导函数求切线方程,以及通过导函数判断函数的单调性和极值等知识点。
(1)当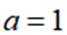
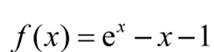
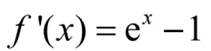
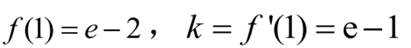
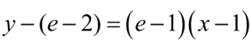
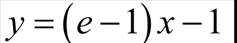
(2)导函数:
当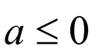
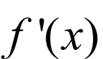
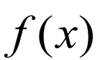
当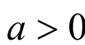
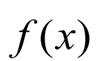
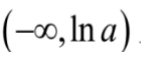
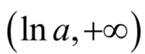
则极小值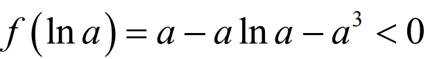
所以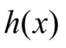

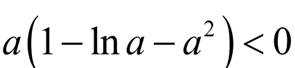
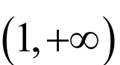
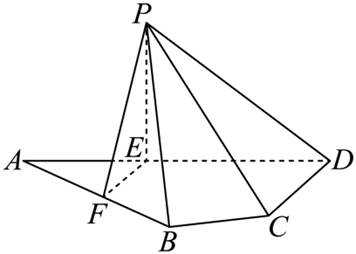
如图,平面四边形ABCD中,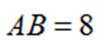
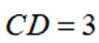
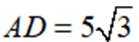
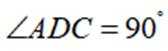
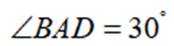
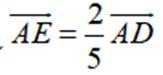
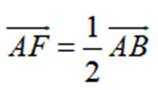
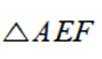
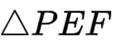
(1)证明:
(2)求面PCD与面PBF所成的二面角的正弦值.
正确答案
(1)
(2)
解析
本题主要考查了平面向量的应用、空间直线与直线的垂直关系的证明、空间向量求二面角等知识点。
(1)证明:设 A的坐标为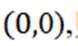
依次求出
P关于EF的中点M对称,
设
将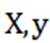
建立坐标系求出各点坐标,再利用向量相乘之积为证明垂直
(2)以E为坐标原点,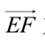

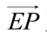
坐标系。
平面PBF交坐标轴于P,E,A三点,坐标分别为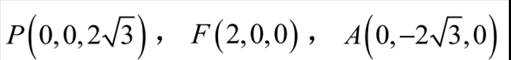
所以平面PBF的平面方程为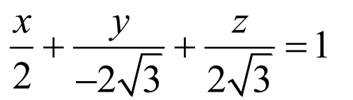
所以平面PBF的法向量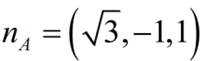
平面PCD平行于X轴,与y轴的交点为D,与Z轴的交点为 P;
所以平面PCD的平面方程为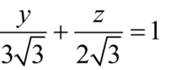
所以平面PCD的法向量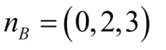
平面PCD与平面PBF所成的二面角的余弦值
所以平面PCD与平面PBF所成的二面角的正弦值为
某投篮比赛分为两个阶段,每个参赛队由两名队员组成,比赛具体规则如下:第一阶段由参赛队中一名队员投篮3次,若3次都未投中,则该队被淘汰,比赛成员为0分;若至少投中一次,则该队进入第二阶段,由该队的另一名队员投篮3次,每次投中得5分,未投中得0分.该队的比赛成绩为第二阶段的得分总和.某参赛队由甲、乙两名队员组成,设甲每次投中的概率为p,乙每次投中的概率为q,各次投中与否相互独立.
(1)若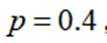
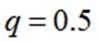
(2)假设
(i)为使得甲、乙所在队的比赛成绩为15分的概率最大,应该由谁参加第一阶段比赛?
(ii)为使得甲、乙,所在队的比赛成绩的数学期望最大,应该由谁参加第一阶段比赛?
正确答案
(1)0.686
(2)(i)甲
(ii)甲
解析
本题主要考查了概率的计算、相互独立事件概率的乘法公式、条件概率,以及对数学期望的理解和计算等知识点。
甲,乙不少5的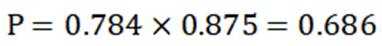
(2)
所以甲>乙
甲获胜概率大
又考虑比较二者乘积大小
所以甲获胜概率大
已知双曲线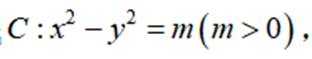
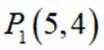
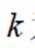
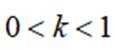

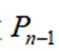
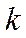
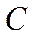

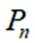
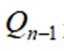
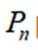
(1)若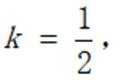
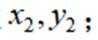
(2)证明:数列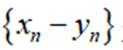
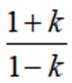
(3)设
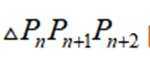
正确答案
(1)
(2)略
(3)略
解析
本题主要考查了双曲线的性质、直线方程、对称点的求法、等比数列的证明、三角形面积的计算等知识点。
得
(2) 由
得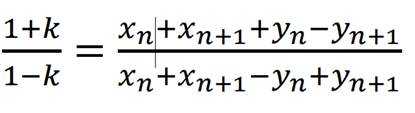
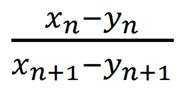
其中倒数第二个等号应用了
这是来自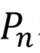
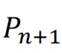
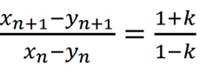
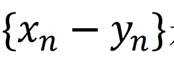
(3)
利用等比
又因为