8.某学校共有老、中、青职工200人,其中有老年职工60人,中年职工人数与青年职工人数相等.现采用分层抽样的方法抽取部分职工进行调查,已知抽取的老年职工有12人,则抽取的青年职工应有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下: 则y对x的线性回归方程为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.r是相关系数,则结论正确的个数为( )
①r∈[-1,-0.75]时,两变量负相关很强
②r∈[0.75,1]时,两变量正相关很强
③r∈(-0.75,-0.3]或[0.3,0.75)时,两变量相关性一般
④r=0.1时,两变量相关很弱
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
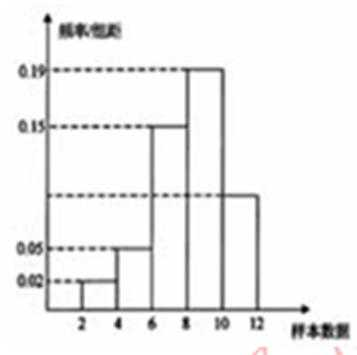
3.有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在区间
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知x,y之间的一组数据如下表,则y与x的线性回归方程y=a+bx必经过点( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.从2009名学生中选取50名学生参加数学竞赛,若采用下面方法选取:先用简单随机抽样从2009人中剔除9人,剩下的2000人,再按系统抽样的方法抽取50人,则在2009人中,每个人入选的机会( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在三维柱形图中,主对角线上两个柱形高度的乘积与副对角线上的两个柱形的高度的乘积相差越大两个变量有关系的可能性就( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
根据上表可得回归直线方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.统计中有一个非常有用的统计量
则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.下面哪些变量是相关关系( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.一位母亲记录了她的儿子3~9岁的身高数据,并由此建立身高与年龄的回归模型为y=7.19x+73.93,用这个模型预测她的儿子10岁时的身高,则正确的叙述是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某校的研究性学习小组为了研究中学生的身高与性别情况,在该校随机抽出80名17至18周岁的学生,其中身高
(1)根据以上数据建立一个
(2)请问在犯错误的概率不超过0.001的前提下,该校17至18周岁的学生的身高与性别是否有关?
参考公式:
参考数据:
正确答案
(1)
(2)
所以,在犯错误的概率不超过0.10的前提下,认为该校17至18周岁的学生身高与性别有关
解析
解析已在路上飞奔,马上就到!
知识点
20.吸烟有害健康,现在很多公共场所都在明令禁止吸烟,为研究是否喜欢吸烟与性别之间的关系,在某地随机抽取400人调研,得到列联表:
试利用独立性检验作出判断.
(参考公式及数据:
正确答案
所以在犯错概率不超过0.001前提下可认为是否吸烟与性别有关
解析
解析已在路上飞奔,马上就到!
知识点
17.为了探究患慢性气管炎与吸烟有无关系,调查了却339名50岁以上的人,结果如下表所示,据此数据请问:50岁以上的人患慢性气管炎与吸烟习惯有关系吗?
正确答案
设患慢性气管炎与吸烟无关.
a=43,b=162,c=13,d=121,a+b=205,c+d=134,
a+c=56,b+d=283,n=339
所以

因此
故有99%的把握认为患慢性气管炎与吸烟有关.
解析
解析已在路上飞奔,马上就到!
知识点
18.某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率
正确答案
(1)从小学、中学、大学中分别抽取的学校数目为3,2,1.
(2)①在抽取到的6所学校中,3所小学分别记为A1,A2,A3,2所中学分别记为A4,A5,大学记为A6,则抽取2所学校的所有可能结果为{A1,A2},{A1,A3},{A1,A4},{A1,A5},{A1,A6},{A2,A3},{A2,A4},{A2,A5},{A2,A6},{A3,A4},{A3,A5},{A3,A6},{A4,A5},{A4,A6},{A5,A6},共15种.
②从6所学校中抽取的2所学校均为小学(记为事件B)的所有可能结果为{A1,A2},{A1,A3},{A2,A3},共3种.
所以P(B)=3/15=1/5.
解析
解析已在路上飞奔,马上就到!
知识点
22.在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)
共有100个数据,将数据分组如下表:
(1)画出频率分布表,并画出频率分布直方图;
(2)估计纤度落在

(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
正确答案
(1)
(2)纤度落在

纤度小于1.40的频率约为
(3)总体数据的众数:1.40 中位数:1.408
平均数:

解析
解析已在路上飞奔,马上就到!
知识点
21.已知某校5个学生的数学和物理成绩如下表
(1)假设在对这


(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用



(3)利用残差分析回归方程的拟合效果,若残差和在
参考数据和公式:



残差和公式为:
正确答案
(1)记事件
(2)


回归直线方程为
(3)
所以为”优拟方程”
解析
解析已在路上飞奔,马上就到!
知识点
15.在调查高一年级1500名学生的身高的过程中,抽取了一个样本并将其分组画成频率颁直方图,[160cm,165cm]组的小矩形的高为a,[165cm,170cm]组小矩形的高为b,试估计该高一年集学生身高在[160cm,170cm]范围内的人数____________
正确答案
7500(a+b)
解析
解析已在路上飞奔,马上就到!
知识点
13.某院校甲、乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在甲专业抽取的学生人数为_______人。
正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
14.盐城市教育局为了调查学生在盐城摸底考试中数学答卷中的有关信息,从上次考试的10000名考生的数学试卷中用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图),则10000人的数学成绩在[140,150]段的约是____________人.
正确答案
800
解析
解析已在路上飞奔,马上就到!
知识点
16.下图为80辆汽车通过某一段公路时的时速的频率分布直方图, 则时速大于60的汽车大约有____辆.
正确答案
48
解析
解析已在路上飞奔,马上就到!