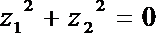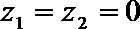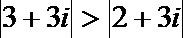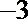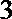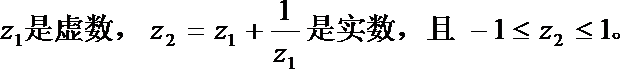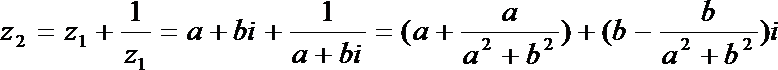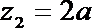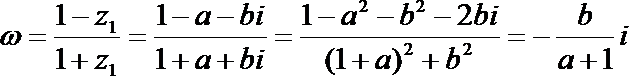数学杨浦区2014年高三试卷

精品

单选题
填空题
简答题

立即下载

数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

3．设复平面上单位圆内接正20边形的20个顶点所对应的复数依次为Z1，Z2，…，Z20，则复数Z，Z，…，Z所对应的不同的点的个数是（）

C10

D20

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

5．向量对应的复数是5-4i，向量对应的复数是-5+4i，则-对应的复数是（）

A-10+8i

B10-8i

C-8+10i

D8-10i

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

7．下列各数中，纯虚数的个数有（）个．

，，，，，

A0个

B1个

C2个

D3个

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

6．下列命题中，正确的是（）

A两个复数不能比较大小

B若，则复数

C虚轴上的点的纵坐标都是纯虚数

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用复数的基本概念复数求模

题型：单选题

分值: 5分

1．若复数是纯虚数，则实数的值为（）

A1或2

B或2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

2．设则复数为实数的充要条件是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：单选题

分值: 5分

4．设复数，若为纯虚数，则实数（）

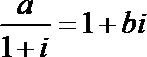
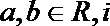
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

8．复数z=（为虚数单位）在复平面内对应的点所在象限为（）

A第一象限

B第二象限

C第三象限

D第四象限

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

9．若等差数列前项和为，则复数在复平面上对应的点位于（）

A第一象限

B第二象限

C第三象限

D第四象限

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：单选题

分值: 5分

11．如果复数的实部和虚部互为相反数，则b的值等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

12．复数（是虚数单位）的虚部是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

10．如果（表示虚数单位），那么（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数的基本概念复数代数形式的乘除运算

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

16．若将复数表示成（a，bR，i是虚数单位）的形式，则____________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：填空题

分值: 5分

13．已知实数满足，则=____________； =____________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：填空题

分值: 5分

15．互为共轭复数，且则=____________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：填空题

分值: 5分

14．在复平面内，复数对应的点位于第____________象限。

正确答案

四

解析

解析已在路上飞奔，马上就到！

知识点

复数的代数表示法及其几何意义复数代数形式的乘除运算

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

22．已知，其中，且为纯虚数．

（1）求的对应点的轨迹；

（2）求的最大值和最小值．

正确答案

（1）设，

则

，

为纯虚数，

即

的对应点的轨迹是以原点为圆心，3为半径的圆，

并除去两点；

（2）由的轨迹可知，，

，圆心对应，半径为3，

的最大值为：，

的最小值为：．

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

18．求同时满足下列条件的所有的复数z，

①z+∈R，且1<z+≤6，

②z的实部和虚部都是整数。

正确答案

设z=x+yi，（x， y∈R），

则z+=x（1+）+y（1－）i ．

∵z+∈R，

∴y（1－）=0．

∴y=0，或x2+y2=10．

又1<z+≤6，

∴1< x（1+）≤6．

① 当y=0时， ①可以化为1<x+≤6，

②当x<0时， x+<0，

当x>0时， x+≥2>6．

故y=0时， ①无解．

当x2+y2=10时， ①可化为1<2x≤6，即<x≤3．

∵x， y∈Z，

故可得z=1+3i ，或 1－3i ，或 3+i ，或 3－i

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

19．m取何值时，复数

（1）是实数；

（2）是纯虚数。

正确答案

（1）

（2）

．

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：简答题

分值: 12分

21．已知，且以下命题都为真命题：

命题实系数一元二次方程的两根都是虚数；

命题存在复数同时满足且．

求实数的取值范围．

正确答案

由命题为真，可得；

由命题为真，可知复平面上的圆和圆有交点，

于是由图形不难得到，

故两个命题同时为真的实数的取值范围是．

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：简答题

分值: 10分

17．设

（1）求 | z1| 的值以及z1的实部的取值范围；

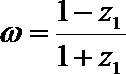
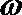
（2）若，求证：为纯虚数。

正确答案

（1）设，则

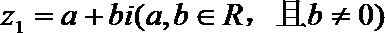
因为 z2是实数，b≠0，

于是有a2+b2=1，即|z1|=1，

还可得

由-1≤z2≤1，得-1≤2a≤1，

解得，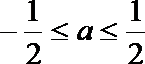

即z1的实部的取值范围是．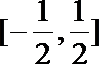

（2）

因为a∈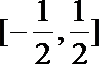，b≠0，

所以为纯虚数．

解析

解析已在路上飞奔，马上就到！

知识点

复数的基本概念复数代数形式的混合运算

题型：简答题

分值: 12分

20．设虚数满足为实常数，，为实数）．

（1）求的值；

（2）当，求所有虚数的实部和；

（3）设虚数对应的向量为（为坐标原点），，如，求的取值范围．

正确答案

（1），

（或）

（2）是虚数，则，

的实部为；

当2．

（3）

① 恒成立，

由得，

当时，；

当时，．

② 如

则

当

．

当

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

数学热门试卷