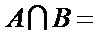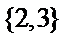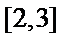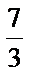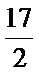已知数列



17.求证:数列
18.若不等式

正确答案
数列
解析
试题分析:本题属于数列与函数的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
证明:

所以数列
考查方向
解题思路
用定义证明等比
易错点
相关知识点不熟容易处错。
正确答案


解析
试题分析:本题属于数列与函数的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
由(1)知,



设



考查方向
解题思路

易错点
相关知识点不熟容易处错。
某游戏网站为了了解某款游戏玩家的年龄情况,现随机调查100位玩家的年龄整理后画出频率分布直方图如图所示。
19.求100名玩家中各年龄组的人数,并利用所给的频率分布直方图估计该款游戏所有玩家的平均年龄;
20.若已从年龄在

正确答案
37岁
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
各组年龄的人数分别为10,30
估计所有玩家的平均年龄为
考查方向
本题考查了利用频率分布直方图求平均值、分层抽样、古典概型等知识点。
解题思路
先求出个组人数,再利用频率分布直方图求平均值
易错点
相关知识点不熟容易出错。
正确答案
解析
试题分析:本题属于概率与统计综合应用问题,属于简单题,只要掌握相关概率与统计的知识,即可解决本题,解析如下:
在





设“这两人在不同年龄组”为事件


考查方向
本题考查了利用频率分布直方图求平均值、分层抽样、古典概型等知识点。
解题思路
先写出基本事件空间,再求出满足条件的基本事件个数,利用古典概型求概率.
易错点
相关知识点不熟容易出错。
如图,在平行四边形ABCD中,AD⊥BD,AD = 2,BD = 4,点M、N分别为BD、BC的中点,将其沿对角线BD折起成四面体QBCD,使平面QBD⊥平面BCD,P为QC的中点。
21.求证:PM⊥BD;
22.求点D到平面QMN的距离。
正确答案
见证明
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:









∴PM⊥BD
考查方向
解题思路
利用相关定理进行证明
易错点
相关定理不熟容易处错。
正确答案
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:


设点D到平面QMN的距离为

所以点D到平面QMN的距离
考查方向
解题思路
利用等体积法即可求解.
易错点
相关定理不熟容易处错。
已知椭圆C:


23.求椭圆C的方程;
24.过点
正确答案
解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
由题意得


考查方向
解题思路
利用相关知识求椭圆方程
易错点
对题中条件的处理容易出错。
正确答案

解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
由题意知直线



得


则



考查方向
本题考查了求椭圆的方程、圆锥曲线中的定值问题等知识点。
解题思路
联立方程组,求出斜率的乘积,整理即可求出定值.
易错点
对题中条件的处理容易出错。
已知函数

25.若

26.已知a < 1,若关于x的不等式
正确答案

解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
函数

设切点

∴切线为:







考查方向
解题思路
先求切线方程,再利用斜率相等即可求a值
易错点
第二问对题中所给条件不知如何下手导致失分。
正确答案

解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
令


当



又







当


即



①当


∴当



②当

综上所述,
考查方向
解题思路
先求导,在分类讨论求实数a的范围.
易错点
第二问对题中所给条件不知如何下手导致失分。
如图,EF是⊙O的直径,AB∥EF,点M在EF上,AM、BM分别交⊙O于点C、D。设⊙O的半径是r,OM = m。
44.证明:
45.若r = 3m,求
正确答案
见解析
解析
作





因为

所以
从而
故
考查方向
解题思路
做辅助线,利用相交弦定理即可证明
易错点
辅助线做不出来导致本题失分。
正确答案

解析
因为


因为
所以
又因为
所以
考查方向
解题思路
利用相交弦定理及三角形相似即可求出
易错点
辅助线做不出来导致本题失分。
4.已知向量a,b满足

正确答案
解析
由



考查方向
解题思路
先由


易错点
对向量运算律不清楚导致出错。
知识点
1.若集合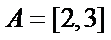
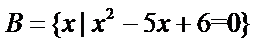
正确答案
解析
由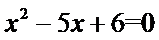
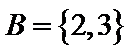
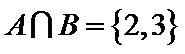
考查方向
解题思路
解一元二次不等式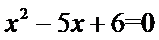
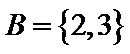
易错点
集合B一元二次不等式不会解导致出错。
知识点
2.若复数z满足zi = 1 + i,则z的共轭复数是
正确答案
解析
容易知道,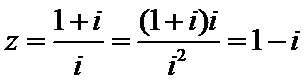
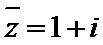
考查方向
解题思路
先求出复数z,再求其共轭复数。
易错点
对复数的运算马虎导致出错。
知识点
3.若m = 6,n = 4,按照如图所示的程序框图运行后,输出的结果
正确答案
解析
由已知m = 6,n = 4知m>n,故y=lg10=1,选择D选项。
考查方向
本题主要考查了程序框图与分段函数的综合应用问题,为高考必考题,在近几年的各省高考题出现的频率较高,常与数列求和、分段函数等知识点交汇命题。
解题思路
根据判断框条件直接计算对数的值。
易错点
对数计算公式不熟悉导致出错。
知识点
5.若函数

正确答案
解析
由



考查方向
解题思路
先求

易错点
忽视自变量的取值范围导致出错。
知识点
7.若点


正确答案
解析
由点



考查方向
解题思路
先根据点



易错点
求
知识点
8.从某大学随机抽取的5名女大学生的身高x(厘米)和体重y(公斤)数据如下表
x 165 160 175 155 170
y 58 52 62 43 60
根据上表可得回归直线方程为
正确答案
解析
由表中的数据可得



考查方向
解题思路
根据所给的表格作出本组数据的样本中心点,根据样本中心点在线性回归直线上,利用待定系数法求出a的值。
易错点
求x,y的平均值时容易导致出错。
知识点
11.双曲线C:




正确答案
解析
如下图所示,由












考查方向
解题思路
先分别求出两个集合中代表元素的取值范围,再求交集。
易错点
对于已知条件
知识点
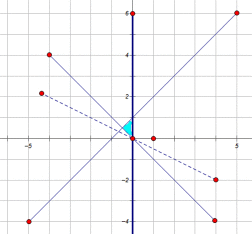
12.在平面直角坐标系xOy中,已知


正确答案
解析
如图,在同一坐标系中画出函数
















考查方向
解题思路
先在同一坐标系中画出函数




易错点
对题中条件不知如何运用导致做本题没有思路。
知识点
6.设


正确答案
解析
由





考查方向
解题思路
先由

易错点
解不等式容易出错。
知识点
9.若函数


正确答案
解析
由函数








考查方向
本题主要考查了正弦型函数的奇偶性及单调性,为高考常考题,在近几年的各省高考题出现的频率较高,常与正弦型函数的单调性、奇偶性、对称性等知识点交汇命题。
解题思路
先由所给函数为偶函数求出
易错点
本题容易直接带区间端点导致值域求错。
知识点
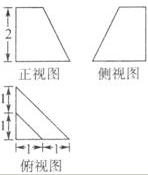
10.已知某几何体的三视图如图所示,则该几何体的表面积为
正确答案
解析
易知,由该几何体的三视图还原后得到原图如下:依题意知该台体ABC-A1B1C1的表面积为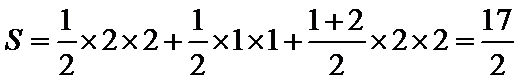
考查方向
解题思路
以三视图为载体考查空间线面位置关系的证明、求解其中一个视图的面积问题、求解几何体的表面积和体积问题等,解决此类问题的关键是能够对给出的三视图进行恰当的分析,从三视图中发现相应的位置关系与数量关系,然后在直观图中解决问.
易错点
不能由三视图还原为原图导致出错。
知识点
13.若实数x,y满足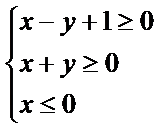
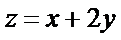
正确答案
2
解析
试题分析:如下图所示,画出可行域,作出直线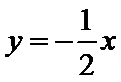
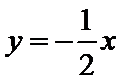
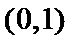
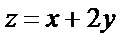
考查方向
解题思路
画出可行域,作出直线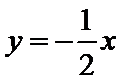
易错点
不能准确画出可行域导致出错。
知识点
14.已知三棱锥P-ABC,若PA,PB,PC两两垂直,且PA = 2,PB = PC = 1,则三棱锥P-ABC外接球的体积为__________。
正确答案
解析
试题分析:该几何体如下图所示,易知,该几何体的外接球的球心在过点M且与平面PBC垂直的直线上,且圆心到点M的距离为1,已知


考查方向
解题思路
先求几何体外接圆的半径,再利用球体积公式求其体积。
易错点
求不出三棱锥外接球的半径导致错误。
知识点
15.已知圆


正确答案
8
解析
试题分析:由




考查方向
解题思路
由




易错点
对题所给条件不知如何应用导致本题没有思路。
知识点
16.已知ΔABC为等边三角形,点M在ΔABC外,且MB = 2MC = 2,则MA的最大值是__________。
正确答案
3
解析
试题分析:如图,以M为坐标原点,建立坐标系,则B(2,0),设

又因为

由


考查方向
解题思路
建立坐标系,利用正余弦定理即可求MA的最大值。
易错点
不知如何建立坐标系,对已知条件不知如何应用导致本题无思路。