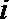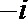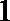4.已知全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若定义在R上的偶函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.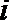
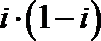
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的侧视图的面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图所示的流程图中,输出的结果是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知平面向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.等差数列{


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若抛物线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA,AC、CB、BP的中点.
(1)求证:D、E、F、G四点共面;
(2)求证:PC⊥AB;
(3)若△ABC和△PAB都是等腰直角三角形,且AB=2,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列






(1)证明
(2)求数列
(3)求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求
(2)说明

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数


(1)求函数
(2)若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.甲、乙二名射击运动员参加今年深圳举行的第二十六届世界大学生夏季运动会的预选赛,他们分别射击了4次,成绩如下表(单位:环):高╗考≧试;题じ库
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加决赛,你认为选派哪位运动员参加比较合适?请说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知动圆过定点

(1)求动圆的圆心轨迹
(2)是否存在直线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.某校高中部有三个年级,其中高三有学生



正确答案
3700
解析
解析已在路上飞奔,马上就到!
知识点
11.设


正确答案
25
解析
解析已在路上飞奔,马上就到!
知识点
13.设



正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14、15题,只能做其中一个,两题全答只计前一题得分)
14.(坐标系与参数方程)
圆C的极坐标方程为
15.(几何证明选讲)
如图,从圆









正确答案
14.
15.
解析
解析已在路上飞奔,马上就到!