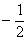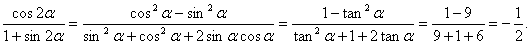1.函数

正确答案
解析
∵



知识点
4.若对任意正实数


正确答案
-1
解析
因为对任意正实数


知识点
6.集合


正确答案
解析
“a=1”是“











知识点
7.已知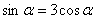
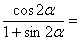
正确答案
解析
由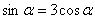
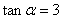
知识点
10.函数
正确答案

解析
因为函数



知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.同时满足(1)
正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
8.方程

正确答案
[-3,1]
解析
解析已在路上飞奔,马上就到!
知识点
9.如果
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知等比数列









正确答案
45
解析
由题意有

































知识点
11.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.关于函数

(2)

(4)

正确答案
(2),(3)
解析
解析已在路上飞奔,马上就到!
知识点
16.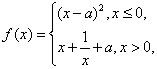
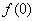
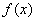
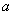
正确答案
解析
由于当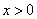
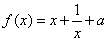
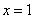
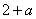

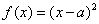
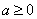
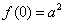
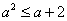
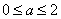
知识点
15.下列说法正确的是( )
正确答案
解析













知识点
17.如果

正确答案
解析

如果



如果


所以 
知识点
18.定义一种新运算:



正确答案
解析
这类问题,首先要正确理解新运算,能通过新运算的定义把新运算转化为我们已经学过的知识,然后解决问题.本题中




























知识点
23.已知函数




(1)求函数
(2)求数列{an}、{bn}的通项公式;
(3)若对任意实数

正确答案
(1)
(2)

(3)3
解析
(1)

(2)∵







(3)对任意实数λ∈[0,1]时,





∴

知识点
22.阅读:
已知



解法如下:
当且仅当

则

应用上述解法,求解下列问题:
(1)已知


(2)已知

(3)已知正数



求证:
正确答案
(1)9;
(2)18;
(3)证明见解析.
解析
(1)
而




(2)







(3)


知识点
21.数列

(1) 求数列
(2) 设





正确答案
(1) 
(2)
解析
(1)





(2)当




知识点
20.在



(1)求
(2)若

正确答案
(1)
(2)
解析
(1)由已知条件结合正弦定理有:


(2)由正弦定理得:



知识点
19.解关于x的不等式:
正确答案
解析
解析已在路上飞奔,马上就到!