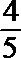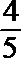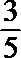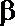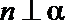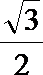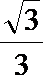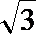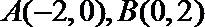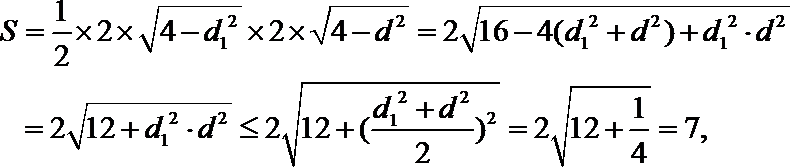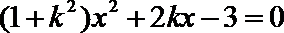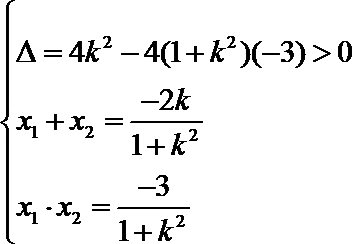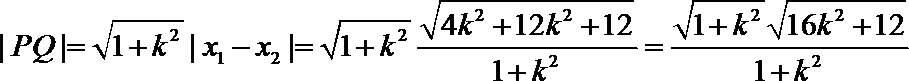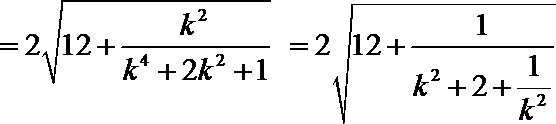1.若
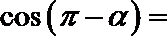
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列四个函数中,在
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.圆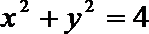
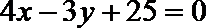
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知向量






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.一个单位有职工160人,其中有业务员104人,管理人员32人,后勤服务人员24人,要从中抽取一个容量为20的样本,用分层抽样的方法抽取样本,则在20人的样本中应抽取管理人员的人数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.为了得到函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.条件

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知三条不同直线
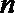



①
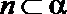

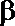
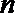
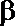

②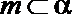
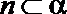
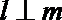
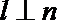
③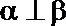
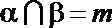
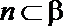

④
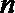
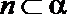

其中正确的命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知某个几何体的三视图(正视图或称主视图,侧视图或称左视图)如图,根据图中标出的尺寸(单位:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.甲、乙两人对一个目标射击,若两人每次击中目标的概率分别为0.7和0.6,则两人同时各射击一次,目标被击中的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.实数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.按照程序框图(如图)执行,第3个输出的数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图为函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.不等式组
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列{an}中,an+1 =

正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
23.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.在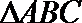
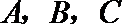
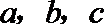

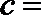
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
24.已知正方体的棱长为1,它的8个顶点都在同一个球面上,那么该球的直径等于__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.在直三棱柱






(Ⅰ)求证
(Ⅱ)求证

(Ⅲ)求异面直线

正确答案
(Ⅰ)(Ⅱ)略(Ⅲ) 
解析
解析已在路上飞奔,马上就到!
知识点
26.已知数列




(Ⅰ)求
(Ⅱ)记





正确答案
(Ⅰ)


①-②得




(Ⅱ)





解析
解析已在路上飞奔,马上就到!
知识点
27.已知圆C经过点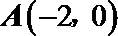
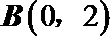
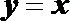
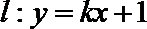
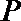

(I)求圆C的方程;
(II)若
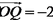
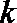
(III)过点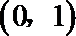

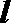
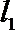
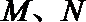

正确答案
(I)设圆心
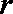
所以
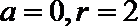
所以圆
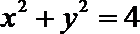
(II)方法一:
因为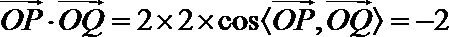
所以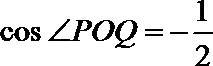
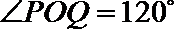
所以圆心到直线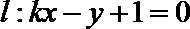
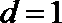
又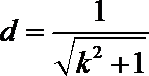
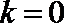
方法二:设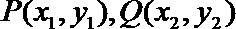
因为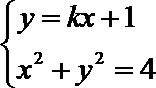
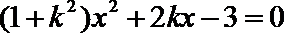
由题意得:
因为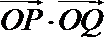
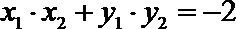
又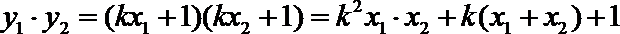
所以, 
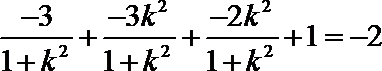
化简得: 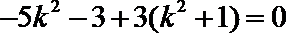
所以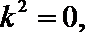
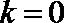
(III)方法一:
设圆心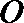

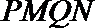
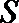
因为直线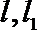
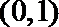
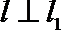
根据勾股定理,有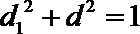
又根据垂径定理和勾股定理得到,
而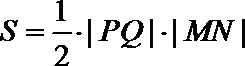
当且仅当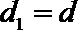
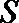
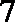
方法二:设四边形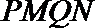
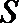
当直线
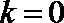

此时
当直线

设
则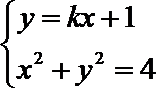
所以
同理得到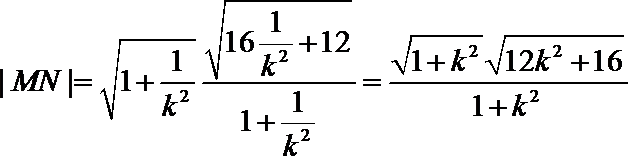
因为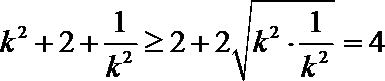
所以 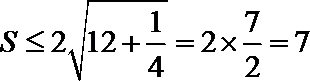
当且仅当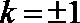
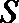

解析
解析已在路上飞奔,马上就到!