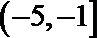1.已知集合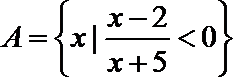
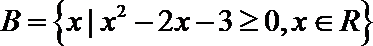
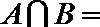
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
5.设复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如图,在直三棱柱



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.某学校高一、高二、高三共有2400名学生,为了调查学生的课余学习情况,拟采用分层抽样的方法抽取一个容量为120的样本.已知高一有820名学生,高二有780名学生,则在该学校的高三应抽取( )名学生.
正确答案
40
解析
解析已在路上飞奔,马上就到!
知识点
11.在极坐标系中,定点A

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如图,三行三列的方阵中有9个数
则至少有两个数位于同行或同列的概率是( ). (结果用分数表示)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.对于集合






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如图所示,在边长为2的正六边形






正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
15.已知直线



①
②
③
④
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设圆O1和圆O2是两个相离的定圆,动圆P与这两个定圆都相切,则圆P的圆心轨迹可能是
①两条双曲线;
②一条双曲线和一条直线;
③一条双曲线和一个椭圆。
以上命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图所示,某旅游景点有一座风景秀丽的山峰,山上有一条笔直的山路BC和一条索道AC,小王和小李打算不坐索道,而是花2个小时的时间进行徒步攀登。已知



正确答案
由

由正弦定理得
所以,
在
由余弦定理得:
即
即
解得

由于
解析
解析已在路上飞奔,马上就到!
知识点
22.定义:对于函数








(1)证明函数

(2)试求一个函数





(3)设函数






正确答案
(1)

所以函数
(2)设
(非零常数) 所以
(3)
所以

设

由

又







由


又




而


解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆
(1)求椭圆
(2)已知直线








正确答案
(1)设椭圆的短半轴为

则


由


(2)由
设
=
=

当


使得
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,△













(1)求该几何体中间一个空心球的表面积的大小;
(2)求图中阴影部分绕直线
正确答案
(1)连接

设

在

所以
所以
(2)





解析
解析已在路上飞奔,马上就到!
知识点
23.一个三角形数表按如下方式构成(如图:其中项数




(1)求第2行和第3行的通项公式

(2)证明:数表中除最后2行外每一行的数都依次成等差数列,并求


(3)若






正确答案
(1)
(2)由已知,第一行是等差数列,假设第

则由


且其公差为
由于
所以
所以


得
于是
即
,又因为
所以,数列
所以,
所以

(3)

令



令
则当


解析
解析已在路上飞奔,马上就到!