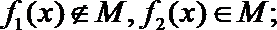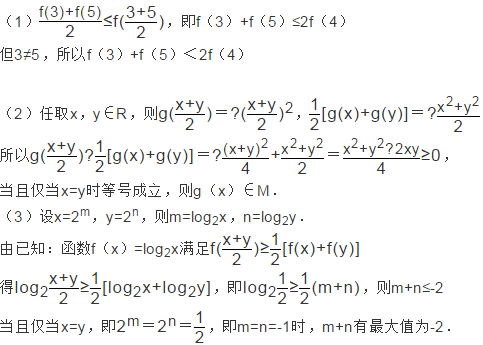数学浦东新区2012年高三试卷

精品

填空题
单选题
简答题

立即下载

数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、单选题

3、简答题

真题试卷
模拟试卷

填空题本大题共14小题，每小题4分，共56分。把答案填写在题中横线上。

题型：填空题

分值: 4分

2．表示为=（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

定积分

题型：填空题

分值: 4分

3．过点A（2，-3），且法向量是的直线的点方向式方程是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

题型：填空题

分值: 4分

8．点A（3，1）和B（-4，6）在直线的两侧，则a的取值范围是（）。

正确答案

（-7，24）

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 4分

9．设的展开式各项系数之和为展开式的二项式系数之和为，则=（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

分值: 4分

10．函数的图像恒过定点A，若点A在直线上，则的最小值是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

分值: 4分

1．已知集合U={1，2，3，4，5}，A={2，4}，B={4，5}，则=（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

分值: 4分

4．若，则x=（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

5．以F1（-3，0）、F2（3，0）为焦点，渐近线方程为的双曲线的标准方程是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：填空题

分值: 4分

6．在等差数列中，若公差，且成等比数列，则公比q=（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

运用诱导公式化简求值

题型：填空题

分值: 4分

7．已知是平面上两上不共线的向量，向量，若，则实数m=（）。

正确答案

-6

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积坐标表示的应用

题型：填空题

分值: 4分

12．一个不透明的袋中装有5个白球、4个红球（9个球除颜色外其余完全相同），经充分混合后，从袋中随机摸出3球，则摸出的3球中至少有一个是白球的概率为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

题型：填空题

分值: 4分

14．若直角坐标平面内的两点P、Q满足条件：

①P、Q都在函数的图像上；

②P、Q关于原点对称，则答点对（P，Q）是函数的一个“友好点对”（点对（P，Q）与（Q，P）看作同一个“友好点对”）。

已知函数则此函数的“友好点对”有（）对。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 4分

11．已知长方体的三条棱长分别为1，1，2，并且该长方体的八个顶点都在一个球的球面上，则此球的表面积为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

13．已知数列是以3为公差的等差数列，是其前n项和，若是数列中的唯一最小项，则数列的首项的取值范围是（）。

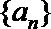
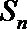
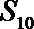
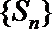
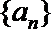
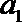
正确答案

（-30，-27）

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

单选题本大题共4小题，每小题5分，共20分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

16．已知程序框图如图所示，则该程序框图的功能是（）

A求数列的前10项和

B求数列的前10项和

C求数列的前11项和

D求数列的前11项和

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的定义域

题型：单选题

分值: 5分

18．若的面积则夹角的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

15．已知实数，则“线性方程组有无穷多组解”是“a、b、c成等比数列”的（）

A充分非必要条件

B必要非充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化

题型：单选题

分值: 5分

17．如图，正方体ABCD—A1B1C1D1的棱长为6，动点E、F在棱A1B1上，动点P、Q分别在棱AB、CD上，若EF=2，DQ=x，AP=y，则四面体PEFQ的体积（）

A与x，y都无关

B与x有关，与y无关

C与x、y都有关

D与x无关，与y有关

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

19．已知关于t的方程一个根为

（1）求方程的另一个根及实数a的值；

（2）若上恒成立，试求实数m的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 14分

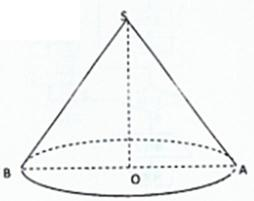
20．用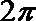平方米的材料制成一个有盖的圆锥形容器，如果在制作过程中材料无损耗，且材料的厚度忽略不计，底面半径长为x，圆锥母线的长为y。

（1）建立y与x的函数关系式，并写出x的取值范围；

（2）圆锥的母线与底面所成的角大小为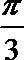，求所制作的圆锥容器容积多少立方米（精确到0.01m3）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：简答题

分值: 16分

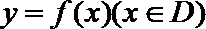
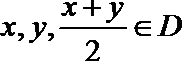
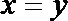
22．我们将具有下列性质的所有函数组成集合M：函数，对任意均满足，当且仅当时等号成立。

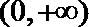
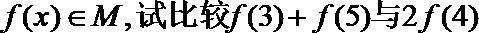
（1）若定义在上的函数大小；

（2）给定两个函数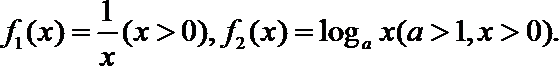：证明：

（3）试利用（2）的结论解决下列问题：若实数m，n满足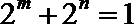，求m+n的最大值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：简答题

分值: 18分

23．定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比。已知椭圆

（1）若椭圆判断C2与C1是否相似？如果相似，求出C2与C1的相似比；如果不相似，请说明理由；

（2）写出与椭圆C1相似且短轴半轴长为b的焦点在x轴上的椭圆Cb的标准方程；若在椭圆Cb上存在两点M、N关于直线对称，求实数b的取值范围？

（3）如图：直线与两个“相似椭圆”分别交于点A，B和点C，D，试在椭圆M和椭圆上分别作出点E和点F（非椭圆顶点），使和组成以为相似的两个相似三角形，写出具体作法。（不必证明）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数单调性的应用

题型：简答题

分值: 14分

21．在数列中，

（1）设，求数列的通项公式；

（2）记数列的前n项和为，试比较的大小。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

数学热门试卷