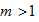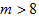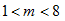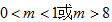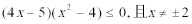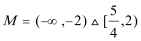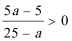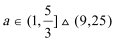1.含有三个实数的集合可表示为{a,1,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知数列{






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.定义;称






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数y=f(x)和y=g(x)在[-2,2]上的图像如图所示,给出下列四个命题
①方程f[g(x)]=0有且仅有6个根
②方程g[f(x)]=0有且仅有3个根
③方程f[f(x)]=0有且仅有5个根
④方程g[g(x)]=0有且仅有4个根,
其中正确的命题个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.对于任意


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.满足条件

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知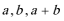
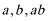
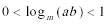
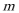
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.定义在R上的函数f(x)满足f(x)= 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若数列


正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
16.设f(x)是定义在R上的奇函数,且


正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
15.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知关于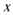
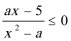
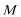
(1)当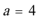
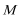
(2)若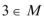
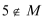
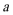
正确答案
(1)当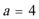
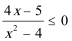
解之,得:
(2)由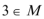
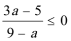
由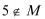
所以得
解析
解析已在路上飞奔,马上就到!
知识点
18.在等差数列


(1)求数列
(2)记


正确答案
(1)设公差为d,由
因为

所以
(2)由(1)得

当


1 -②得
所以
解析
解析已在路上飞奔,马上就到!
知识点
19.已知

(1)求

(2)若当


正确答案
(1)因为
即
设



又

,即
(2)

得
由

解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列


(1)求

(2)设

正确答案
(1)

①- ②得


所以,

所以


(2)
所以


又因为

又因为对于一切正整数n都有


解析
解析已在路上飞奔,马上就到!
知识点
22.已知数列





(I)求
(Ⅱ)设:




(Ⅲ)对于(Ⅱ)中的





正确答案
(I)由于
所以有:

而:

所以


(Ⅱ)

所以数列
由前


所以有
(Ⅲ)由于
又因为
所以有:






但是,

所以只有当

解析
解析已在路上飞奔,马上就到!
知识点
21.已知集合


(1)若

(2)若方程


正确答案
(1)若






设

所以实数
(2)方程



即在


当

所以实数
解析
解析已在路上飞奔,马上就到!