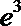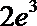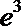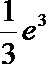1.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设曲线y=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设平面区域D是由双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若曲线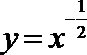
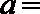
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设函数的定义域为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.曲线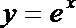
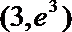
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.如下图,阴影部分的面积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.由曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知


正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)若函数


(2)设函数




正确答案
(1)由题意知,

由
∵
令
故

其值域为
∴ 
(2)∵
由已知得:

即
当
当

令
由于二次函数
故它在闭区间上的最小值必在区间端点处取得,
又
∴ 不等式②恒成立的充要条件是
即

∵ 这个关于

∴ 
即

又
从而

解析
解析已在路上飞奔,马上就到!
知识点
18.定义函数
(1)令函数



(2)令函数

在

(3)当


正确答案
(1)
由

又
由


又


存在与直线
其方程为
即
(2)
由

由

在


得


而
当且仅当

(3)证明:

令
则
当

∴ 




又当

当


即
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(Ⅰ)若曲线



(Ⅱ)求
(Ⅲ)设




正确答案
(Ⅰ)
(Ⅱ)
①当

在区间
在区间
故

②当
在区间

在区间
故


③当

故
④当
在区间

在区间
故


(Ⅲ)由已知,在
由已知,
①当


故
所以,
故
②当



故
由
所以
综上所述, 
解析
解析已在路上飞奔,马上就到!
知识点
20.设函数
(1) 求函数
(2) 设

(3) 斜率为




正确答案
(1)
令
∵ 当
当
∴ 当
(2)
① 当



② 当


令

综上,当


当



(3)
要证
等价于证
则只要证

故等价于证
① 设
故

∴ 当

② 设



∴ 当

由①②知(*)成立,得证
解析
解析已在路上飞奔,马上就到!
知识点
21.已知




(1)求


(2)求证
(3)求


正确答案
(1)



又
因为 
又因为 
所以
又因为 
所以
即

所以
(2)因为
所以
所以
(3)因为

所以
所以
又因为
所以
当且仅当
所以
解析
解析已在路上飞奔,马上就到!
知识点
17.设函数


(1)求a、b的值;
(2)若对于任意的

正确答案
(1)
解得
(2)由(1)可知,
当
即




又
故当


于是有

因此
解析
解析已在路上飞奔,马上就到!