1.满足{1,2}
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
4.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知
正确答案
0.6
解析
解析已在路上飞奔,马上就到!
知识点
6. 若集合A={

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知m∈R,复数z=m2+4m+3+(m2 +2m-3)i ,当m=________时,z是纯虚数
正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
8.函数y=x2-3x(x<1)的反函数是___________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设等差数列



正确答案
45
解析
解析已在路上飞奔,马上就到!
知识点
9.已知f(x)=log
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内只有一个盒子空着,共有____________种投放方法?
正确答案
1200
解析
解析已在路上飞奔,马上就到!
知识点
11.若









正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
12.设直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.下列命题中的真命题为______________________
(1) 复平面中满足|z-2|-|z+2|=1的复数
(2) 当

(3)已知函数



(4)在平面直角坐标系


(5) 设平面直角坐标系xoy中方程F(x,y)=0表示一个椭圆,则总存在实常数p、q,使得方程F(px , qy)=0表示一个圆。
正确答案
(2)(3)(4)
解析
解析已在路上飞奔,马上就到!
知识点
16.已知二次函数y=a(a+1)x2-(2a+1)x+1,当a=1,2,…,n,…时,其抛物线在x轴上截得的线段长依次为d1,d2,…,dn,…,则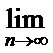
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数y=logax当x>2 时恒有
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a, DC=a,F、G分别为EB和AB的中点.
(1)求证:FD∥平面ABC;
(2) 求二面角B—FC—G的正切值.
正确答案
(1)略
(2)
解析
解析已在路上飞奔,马上就到!
知识点
18.已知
(1)求sinx-cosx的值;
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.若α,β是实系数方程x2+x+p=0 的二根,|α-β| =3,则求实数p的值及方程的根。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列{an}满足条件:a1=1,a2=r(r>0),且{anan+1}是公比为q(q>0)的等比数列,设bn=a2n-1+a2n(n=1,2,…).
(1)求出使不等式anan+1+an+1an+2>an+2an+3(n∈N*)成立的q的取值范围;
(2)求bn和
(3)设r=219.2-1,q=

正确答案
(1)
(2)
(3)最大项2.25 ,最小项-4
解析
解析已在路上飞奔,马上就到!
知识点
20.某县一中计划把一块边长为20米的等边三角形ABC的边角地辟为植物新品种实验基地,图中DE需把基地分成面积相等的两部分,D在AB上,E在AC上.
(1)设AD=x(x≥10),ED=y,试用x表示y的函数关系式;
(2)如果DE是灌溉输水管道的位置,为了节约,则希望它最短,DE的位置应该在哪里?如果DE是参观线路,则希望它最长,DE的位置又应该在哪里?说明理由
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
22.已知复数



(1)若复数




(2) 将(1)中的轨迹上每一点按向量



(3) 过轨迹C上任意一点A(异于顶点)作其切线,交y轴于点B,求证:以线段AB为直径的圆恒过一定点,并求出此定点的坐标。
正确答案
(1)
(2)
(3)定点(1,0)
解析
解析已在路上飞奔,马上就到!


























