数学北碚区2015年高三试卷

精品

单选题
填空题
简答题

立即下载

数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．已知集合，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

交集及其运算指数函数单调性的应用

题型：单选题

分值: 5分

5．若的展开式中前三项的系数成等差数列，则展开式中的有理项共有（）

A2项

B3项

C4项

D5项

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求二项展开式的指定项或指定项的系数

题型：单选题

分值: 5分

9．如图，设P、Q为△ABC内的两点，且，，则△ABP的面积与△ABQ的面积之比为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的基本定理及其意义向量在几何中的应用

题型：单选题

分值: 5分

10．已知函数，记为的导函数，若在R上存在反函数，且b > 0，则的最小值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值及其几何意义反函数导数的运算

题型：单选题

分值: 5分

2．的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的恒等变换及化简求值诱导公式的作用两角和与差的正弦函数

题型：单选题

分值: 5分

3．已知双曲线的中心在原点，一个焦点为，点P位于该双曲线上，线段PF1的中点坐标为，则双曲线的方程为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：单选题

分值: 5分

4．已知，现有下列不等式：

①；

②；

③；

④，

其中正确的是（）

A②④

B①②

C③④

D①③

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用对数值大小的比较不等式的性质利用基本不等式求最值

题型：单选题

分值: 5分

6．已知直线与圆交于两点A、B，且，其中O为坐标原点，则实数a的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的模向量在几何中的应用直线与圆相交的性质

题型：单选题

分值: 5分

7．设曲线在点（2，）处的切线与x轴交点的横坐标为an，则数列的前n项和为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义导数的运算错位相减法求和数列与函数的综合

题型：单选题

分值: 5分

8．定义在R上的函数，则的值为（）

A– 1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

分段函数的解析式求法及其图象的作法函数的周期性函数的值

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11．设向量满足，则的夹角是_________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算数量积表示两个向量的夹角量积判断两个平面向量的垂直关系

题型：填空题

分值: 5分

12．已知实数x、y满足，则目标函数的最小值为______．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

其它不等式的解法

题型：填空题

分值: 5分

14．由1，2，3，4，5组成的五位数字，恰有2个数位上的数字重复且十位上的数字大于百位上的数字的五位数的个数是_________．（用数字作答）

正确答案

540

解析

解析已在路上飞奔，马上就到！

知识点

排列、组合及简单计数问题

题型：填空题

分值: 5分

13．已知抛物线的焦点F恰好是双曲线的右焦点，且两条曲线交点的连线过点F，则该双曲线的离心率为________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的几何性质抛物线的标准方程和几何性质

题型：填空题

分值: 5分

15．有四个命题：

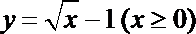
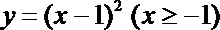
①函数的反函数是；

②函数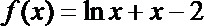的图象与x轴有两个交点；

③函数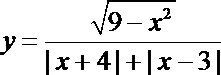的图象关于y轴对称；

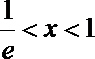
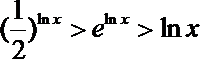
④若，则．

其中真命题的序号是________．

正确答案

③④

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用奇偶函数图象的对称性对数的运算性质反函数

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 13分

17.已知向量，，定义

（1）求出的解析式．当时，它可以表示一个振动量，请指出其振幅，相位及初相．

（2）的图像可由的图像怎样变化得到？

（3）设时的反函数为，求的值．

正确答案

（1）

其振幅为，相位为，初相为

（2）可由图象横坐标不变，纵坐标伸长到原来的倍，再把曲线上所有的点向左平移个单位，即可得的图象．

（3）由得

∵ ∴ ∴ ∴

∴

解析

解析已在路上飞奔，马上就到！

知识点

反函数函数y=Asin（ωx+φ）的图象变换y=Asin（ωx+φ）中参数的物理意义三角函数中的恒等变换应用平面向量数量积的运算

题型：简答题

分值: 13分

19.已知数列{bn}的前n项和．数列{an}满足，数列{cn}满足．

（1）求数列{an}和数列{bn}的通项公式；

（2）若对一切正整数n恒成立，求实数m的取值范围．

正确答案

（1）当时，

又适合上式

∴

由

（2）

∵

∴ ，即

∴ {cn}的最大项为

∴

∴ 实数m的取值范围为

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式错位相减法求和数列与不等式的综合

题型：简答题

分值: 12分

20.若，且．

（1）求的最小值及对应的x值；

（2）若不等式的解集记为A，不等式的解集记为B，求．

正确答案

（1） ∵

∴ ，∴

∴ a = 2或a = 1（舍）

又 ∵

∴ ∴ b = 2

∴ ，

∴ 当时，的最小值为

（2）由

∴

∴ ，即

由

∴

解析

解析已在路上飞奔，马上就到！

知识点

交集及其运算二次函数的图象和性质对数的运算性质其它不等式的解法

题型：简答题

分值: 13分

16．已知向量，且，其中A、B、C是△ABC的内角，a、b、c分别是角A、B、C的对边．

（1）求角C的大小；

（2）求的取值范围．

正确答案

（1）由得，

即

由余弦定理得

∵

∴

（2） ∵

∴

∵ ∴

∴

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理平面向量数量积的运算

题型：简答题

分值: 12分

21.如图，椭圆C：的焦点在x轴上，左、右顶点分别为A1、A，上顶点为B．抛物线C1、C2分别以A、B为焦点，其顶点均为坐标原点O，C1与C2相交于直线上一点P．

（1）求椭圆C及抛物线C1、C2的方程；

（2）若动直线l与直线OP垂直，且与椭圆C交于不同两点M、N，已知点，求的最小值．

正确答案

（1）由题意得A（a，0），B（0，）

∴ 抛物线C1的方程可设为；抛物线C2的方程可设为

由

代入得a = 4

∴ 椭圆方程为，抛物线C1：，抛物线C2：

（2）由题意可设直线l的方程为

由消去y得

由

设M（x1，y1），N（x2，y2），则

∵

∴

∵

∴ 当时，其最小值为

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算椭圆的定义及标准方程抛物线的标准方程和几何性质圆锥曲线中的范围、最值问题直线、圆及圆锥曲线的交汇问题

题型：简答题

分值: 12分

18. 已知函数的图象在以点为切点的切线的倾斜角为

（1）求m、n的值；

（2）求函数在上的最大值和最小值．

正确答案

（1），由题意得

∴ 解得

（2），由得

当x变化时，的变化情况如下：

∴

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

数学热门试卷