数学昆明市2015年高三试卷

精品

单选题
填空题
简答题

立即下载

数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．复数满足（为虚数单位），则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

3．设，向量，且//，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

4．在展开式中的系数为，则实数的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

5．在各项均为正数的等比数列中，成等差数列，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：单选题

分值: 5分

11．三棱锥的外接球为球，球的直径，且都是等边三角形，则三棱锥的体积是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：单选题

分值: 5分

9．设满足约束条件，若目标函数的最大值为，则的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

1．已知集合，则（）

A{-3，-2，-1，0，1}

B{-2，-1，0，1}

C{-2，-1，0}

D{-1，0，1，2}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

6．某程序框图如图所示，该程序运行后输出的值是（）

C100

D102

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面的基本性质及推论

题型：单选题

分值: 5分

10．已知为抛物线上一个动点，为圆上一个动点，那么点到点的距离与点到轴距离之和的最小值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间图形的公理

题型：单选题

分值: 5分

12．设函数，则函数的各极小值之和为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：单选题

分值: 5分

7．曲线在处的切线方程是，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数幂的运算

题型：单选题

分值: 5分

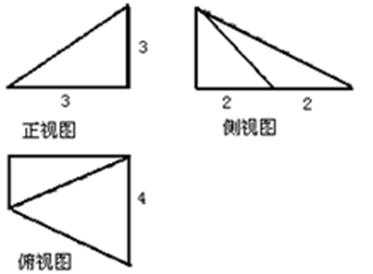
8．如图是一几何体的三视图，则该几何体的体积是（）

B10

C12

D18

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的图象和性质

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

13．已知，则____________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

16．已知实数，若函数的图象与函数的图象有两个不同的交点，则的取值范围为____________

正确答案

1<a<e

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 5分

15．若函数对任意的恒成立，则的取值范围是____________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数图象的应用

题型：填空题

分值: 5分

14．两所学校分别有2名、3名学生获奖，这5名学生要排成一排合影，则同校学生排在一起的概率是____________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

一元高次不等式的解法

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

18．如图所示，在四棱锥中，底面为菱形，为的中点．

（1）若，求证：平面平面；

（2）点在线段上，二面角为，若平面平面，且，求三棱锥的体积．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平行公理

题型：简答题

分值: 12分

19．甲、乙两支球队进行总决赛，比赛采用五场三胜制，即若有一队先胜三场，则此队为总冠军，比赛就此结束．因两队实力相当，每场比赛两队获胜的可能性均为二分之一．据以往资料统计，第一场比赛可获得门票收入40万元，以后每场比赛门票收入比上一场增加10万元．

（1）求总决赛中获得门票总收入恰好为220万元的概率；

（2）设总决赛中获得的门票总收入为，求的分布列和数学期望．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 12分

20．已知椭圆的离心率为，且抛物线的焦点恰好是椭圆的一个焦点．

（1）求椭圆的方程；

（2）过点作直线与椭圆交于两点，点满足（为原点），求四边形面积的最大值，并求此时直线的方程．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：简答题

分值: 10分

选做题：请考生在第22，23，24三题中任选一题做答，如果多做，则按所做的第一题计分．

22．选修：几何证明选讲

如图，为直角三角形，，以为直径的圆交于点，点是边的中点，连接交圆于点．

求证：

（1）四点共圆；

（2）．

23．选修：坐标系与参数方程

在直角坐标系中，半圆的参数方程为（为参数，）．以为极点，轴的非负半轴为极轴建立极坐标系．

（1）求的极坐标方程；

（2）直线的极坐标方程是，射线与半圆的交点为，与直线的交点为，求线段的长．

24．选修：不等式选讲

在中，内角所对的边的长分别为，

证明：（1）；（2）．

正确答案

22.

23.

24.

解析

解析已在路上飞奔，马上就到！

知识点

指数函数单调性的应用

题型：简答题

分值: 12分

17．在中，角所对的边分别是，已知．

（1）求；

（2）若，且，求的面积．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：简答题

分值: 12分

21．设函数，为常数（），．

（1）若对任意的，恒有，求的取值范围；

（2）对任意的，函数恒成立，求实数的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

数学热门试卷