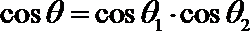1.在北纬45°的纬度圈上有甲、乙两地,两地经度差为90°,则甲、乙两地最短距离为(设地球的半径为R) ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知直线l、m 、n 与平面α、β给出下列四个命题:
① 若m∥l,n∥l,则m∥n;
②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n
④若m⊥β,α⊥β,则m∥α。
其中,假命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.M是空间直角坐标系Oxyz中任一点(异于O),若直线OM与xOy平面,yoz平面,zox平面所成的角的余弦值分别为p, q, r,则p2+q2+r2=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在平行六面体







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.一个二面角的两个面分别垂直于另一个二面角的两个面,那么这两个二面角( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.如图,正方体ABCD—A1B1C1D1的棱长为1,线段AC1上有两个动点E、F,且
①BF//CE;
②CE⊥BD;
③三棱锥E—BCF的体积为定值;
④△BEF在底面ABCD内的正投影是面积为定值的三角形;
其中,正确结构的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.底面是正三角形,且每个侧面是等腰三角形的三棱锥是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.一个正方体的顶点都在球面上,它的棱长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北。现有沿该正方体的一些棱将正方体剪开、外面朝上展平,得到下边的平面图形,则标“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知某几何体的三视图如图所示,其中,正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.棱长为1的正方体

正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
15.一个几何体的三视图如图所示,其中主视图中

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.以下4个命题其中正确的命题是____________
(1)如果一个几何体的三视图是完全相同的,则这个几何体是正方体;
(2)如果一个几何体的主视图和俯视图都是矩形,则这个几何体是长方体;
(3)如果一个几何体的三视图都是矩形,则这个几何体是长方体;
(4)如果一个几何体的主视图和左视图都是等腰梯形,则这个几何体是圆台。
正确答案
(3)
解析
解析已在路上飞奔,马上就到!
知识点
13.已知四面体P-ABC中,PA⊥平面ABC,
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。
(1) 求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=
正确答案
(1)因为PA⊥平面ABCD,
CE∈平面ABCD,所以PA⊥CE,
因为AB⊥AD,CE∥AB,
所以CE⊥AD,又PA∩AD=A,
所以CE⊥平面PAD.
(2)由(1)可知CE⊥AD,
在直角三角形ECD中,
DE=CD

又因为AB=CE=1,AB∥CE,
所以四边形ABCE为矩形,
所以
=
=
又PA⊥平面ABCD,PA=1,
所以四棱锥P-ABCD的体积等于
解析
解析已在路上飞奔,马上就到!
知识点
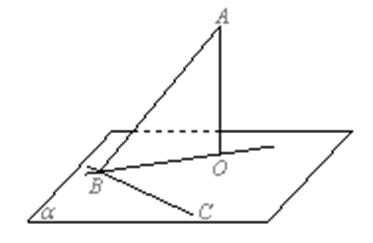
20.如图,已知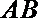


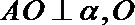


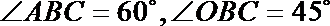


正确答案
∵
由斜线和平面所成角的定义可知
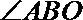

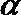
又∵
∴
∴


解析
解析已在路上飞奔,马上就到!
知识点
17.已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.
正确答案
设圆台的母线长为
圆台的上底面面积为
圆台的上底面面积为
所以圆台的底面面积为
又圆台的侧面积
于是
即
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,已知三棱柱








(1)当



(2)若平面



正确答案
(1)以AB,AC,


则
平面ABC的一个法向量为

于是问题转化为二次函数求最值,而




(2)已知给出了平面PMN与平面ABC所成的二面角为
即可得到平面ABC的一个法向量为

设平面PMN的一个法向量为

由
得
解得
令

解得

解析
解析已在路上飞奔,马上就到!
知识点
19.如图,




(Ⅰ)当平面


(Ⅱ)当

正确答案
(Ⅰ)取


因为

当平面

因为平面

所以

由已知可得
在

(Ⅱ)当


证明如下:
①当


所以


②当


又因

又


由


综上所述,总有
解析
解析已在路上飞奔,马上就到!
知识点
22.如图,四棱柱





(1)求证:

(2)求直线

正确答案
(1)证明:四棱柱
又



又


所以平面
所以
(2)解:
因为
所以
如图,以
在
所以
因为
所以
又
所以
所以平面
设


则
所以直线

解析
解析已在路上飞奔,马上就到!