4.




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设



正确答案
-192
解析
解析已在路上飞奔,马上就到!
知识点
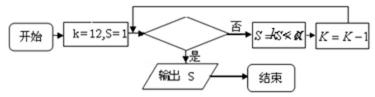
9.程序框图如下:如果上述程序运行的结果为S=132,那么判断框中实数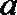
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若
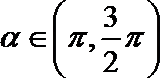
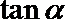
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知定义在





正确答案
-5
解析
解析已在路上飞奔,马上就到!
知识点
7.把10本书随机地排在书架上,则其中指定的3本书排在一起的概率是( ).(结果用分数表示)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设实数



正确答案
121
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数













正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如图,在平面直角坐标系






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.等差数列


正确答案
14
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,相距200海里的A、B两地分别有救援A船和B船。在接到求救信息后,A船能立即出发,B船因港口原因需2小时后才能出发,两船的航速都是30海里/小时.在同时收到求救信息后,A船早于B船到达的区域称为A区,否则称为B区。若在A地北偏东


(1)求A区与B区边界线(即A、B两船能同时到达的点的轨迹)方程;
(2)问:①应派哪艘船前往救援?②救援船最快需多长时间才能与遇险船相遇?(精确到
正确答案
(1)设点
由题意知

即动点


∴点
由

∴方程为

(2)①





∴


∴点
即遇险船始终在A区内,
∴应派A船前往救援
②设经

在

∴
整理得
解得

∴A救援船需
解析
解析已在路上飞奔,马上就到!
知识点
23. 对于数列





(1)首项为1,公比为

(2)若数列

①证明:

②令


正确答案
(1)由已知的等比数列通项公式为
则
所以,该数列是
(2)
①
又
可得
所以,

②因为
所以

+
=
所以,数列

解析
解析已在路上飞奔,马上就到!
知识点
19.已知在正四棱锥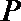


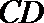
正确答案
设底边长为
故
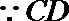
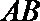



所以,异面直线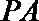

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数




(1)已知关于



(2)当

(3)当




正确答案
(1)转化为求函数

该函数在

所以

(2)

定义域关于原点对称,
又

所以函数
下面讨论在
任取

设

则
所以
因为


所以
又当

所以
由定义知在
又因为函数

(3)


又
令
则方程



所以
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)若函数


(2)若函数


正确答案
(1)

又因为函数

所以

又因为


(2)设

故
解析
解析已在路上飞奔,马上就到!
知识点
15.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设

(1)
(2)
(3)
(4)
与
正确答案
解析
解析已在路上飞奔,马上就到!