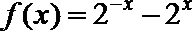1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知点



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.下列说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.定义在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列函数中,在其定义域内,既是奇函数又是减函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.一物体沿直线以速度




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知奇函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知
(Ⅰ)求
(Ⅱ)若

正确答案
(Ⅰ)
(Ⅱ)






解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数

(Ⅰ)求函数

(Ⅱ)证明:无论


正确答案
(Ⅰ)



即
由
又



(Ⅱ)

而直线


即无论


解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(Ⅰ)若实数


(Ⅱ)记函数









正确答案
(Ⅰ)


若





若


当

所以


(Ⅱ)




令


令
当且仅当




解析
解析已在路上飞奔,马上就到!
知识点
18. 提高立交桥的车辆通行能力可改善整个城市的交通状况。在一般情况下,立交桥上的车流速度




(Ⅰ)当

(Ⅱ)当车流密度

正确答案
(Ⅰ)由题意:当

当
再由已知得

故函数
(Ⅱ)依题意并由(Ⅰ)可得
当


当
当


综上,当当


即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
解析
解析已在路上飞奔,马上就到!
知识点
20.设
(Ⅰ)求
(Ⅱ)若



正确答案
(Ⅰ)令











(Ⅱ)



由



故有

当


当


当
综上,实数

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数








(Ⅰ)若


(Ⅱ)求证:
正确答案
(Ⅰ)由题意对定义域内的任意


当

则当

由



当
令
则当
















(Ⅱ)由(Ⅰ)可知,当

则
令



将以上不等式两端分别相加得:
即
解析
解析已在路上飞奔,马上就到!