4．已知三条不重合的直线m、n、l与两个不重合的平面α、β，有下列命题：
①若m∥n，n⊂α，则m∥α；
②若l⊥α，m⊥β且l∥m，则α∥β；
③若m⊂α，n⊂α，m∥β，n∥β，则α∥β；
④若α⊥β，α∩β＝m，n⊂β，n⊥m，则n⊥α．
其中正确的命题个数是（ ）
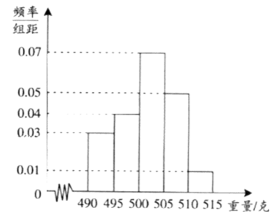
11．某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上的40件产品作为样本称出它们的重量（单位：克），重量的分组区间为（490，495]，（495，500]，……，（510，515]，由此得到样本的频率分布直方图，如图所示．根据此频率分布直方图，可知重量超过500克的产品共有________件．
14．已知
（Ⅰ）若
（Ⅱ）若
16． 在一个选拔项目中，每个选手都需要进行4轮考核，每轮设有一个问题，能正确回答者进入下一轮考核，否则被淘汰． 已知某选手能正确回答第一、二、三、四轮问题的概率分别为
（Ⅰ）求该选手进入第三轮才被淘汰的概率；
（Ⅱ）求该选手至多进入第三轮考核的概率；
（Ⅲ）该选手在选拔过程中回答过的问题的个数记为
17．如图，三棱柱ABC—A1B1C1中，AA1⊥面ABC，BC⊥AC，BC=AC=2，AA1=3，D为AC的中点．
（Ⅰ）求证：AB1//面BDC1；
（Ⅱ）求二面角C1—BD—C的余弦值；
（Ⅲ）在侧棱AA1上是否存在点P，使得CP⊥面BDC1？并证明你的结论．
19．设椭圆
（Ⅰ）若过
（Ⅱ）在（Ⅰ）的条件下，过右焦点
20．对于数集
（Ⅰ）若
（Ⅱ）若X具有性质P，求证：1X，且当
（Ⅲ）若X具有性质P，且
