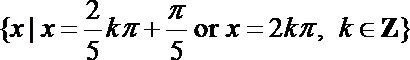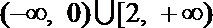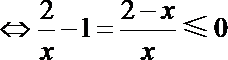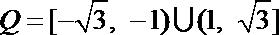1.已知等比数列



正确答案
64
解析




知识点
3.设集合



正确答案
解析




所以
知识点
4.已知函数


正确答案
1
解析
此即
知识点
5.方程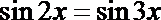
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.不等式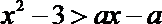
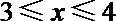
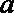
正确答案
3
解析
结合函数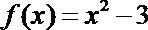
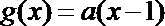
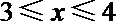
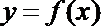
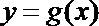
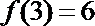
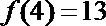
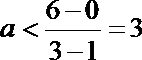
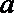
知识点
2.不等式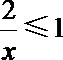
正确答案
解析

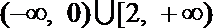
知识点
6.函数
正确答案

解析




知识点
7.若函数



正确答案
解析
在函数




知识点
8.已知等差数列





正确答案
解析
等价于
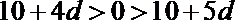

知识点
9.已知函数

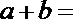
正确答案
1
解析
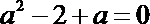
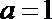


知识点
11.在







正确答案
解析
由正弦定理,得






知识点
14.已知函数
①对任意

②当

若
正确答案
95
解析
由①②知,当




















所以



知识点
12.若函数

正确答案
解析
假若






知识点
13.已知


正确答案
解析
由已知得







知识点
16.若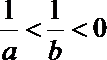
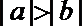
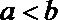
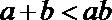
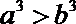
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知:数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 关于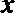
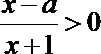
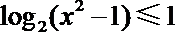
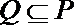
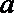
正确答案
当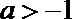
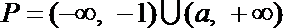
当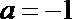
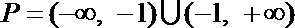
当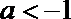
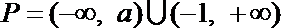
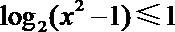
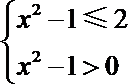
所以
所以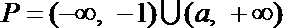
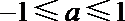
解析
解析已在路上飞奔,马上就到!
知识点
20.已知:函数




(1)求:


(2)若








正确答案
解:(1)
由

由


所以
(2)


所以

所以,函数

解析
解析已在路上飞奔,马上就到!
知识点
21.市场上有一种新型的强力洗衣液,特点是去污速度快。已知每投放a(





(1)若只投放一次4个单位的洗衣液,则有效去污时间可达几分钟?
(2)若第一次投放2个单位的洗衣液,6分钟后再投放


正确答案
解:(1)因为

则当



当



综上,得
(2)当

当且仅当



令

所以

解析
解析已在路上飞奔,马上就到!
知识点
22.设等差数列



(1)求
(2)设



(3)将数列








正确答案
解:(1)因为数列



所以

(2)设



(法二,比差法)因为
所以


因为不等式


(3)数列










其中

解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数


(1)若


(2)若


(3)当


正确答案
(1)对于

所以
当且仅当


(2)


所以

又
故只需



(3)
因为

所以,比较



令




(法一)因为

令

(1)当



(2)当



(3)当



综上所述,
(法二)对于

因为

对于

因为

(1)当


(2)当




又令





综上,
解析
解析已在路上飞奔,马上就到!