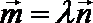2.关于x的不等式:
正确答案
–1<x<2
解析
解析已在路上飞奔,马上就到!
知识点
4.从三名男同学和


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
8.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.关于定义在

(1)若对任意



(2)若对任意



(3)函数


(4)函数


其中正确判定的序号是( )
正确答案
(1)(2)(3)(4)
解析
解析已在路上飞奔,马上就到!
知识点
1.已知f(x)为奇函数,且当x>0时f(x)=x(x–1),则f(–3)=( )
正确答案
–6
解析
解析已在路上飞奔,马上就到!
知识点
3.设





正确答案
(0,9 )
解析
解析已在路上飞奔,马上就到!
知识点
5. 关于x、y的二元线性方程组


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在


正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
7.若直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.经过点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设




正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
12.已知


①长分别为
②长分别为
③长分别为
④长分别为
其中正确命题的序号( )
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
14.对于集合N={1,2,3,…,n}及其它的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数.例如集合{1,2,4,6,9}的交替和是9–6+4–2+1=6,集合{5}的交替和为5.当集合N中的n=2时,集合N={1, 2}的所有非空子集为{1},{2},{1,2},则它的“交替和”的总和



正确答案
n·2(n–1)
解析
解析已在路上飞奔,马上就到!
知识点
17.已知不等式



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.下列所给的四个命题中,不是真命题的为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.点







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知复数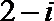
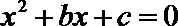
(1)求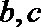
(2)若向量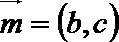
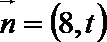
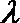
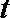
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.
正确答案
(1)

消去

即



即

所以函数

解析
解析已在路上飞奔,马上就到!
知识点
23.函数是这样定义的:对于任意整数



(1)求函数的定义域

(2)若数列


(3)若等比数列




正确答案
(1)函数


(2)由于


(3)由










解析
解析已在路上飞奔,马上就到!
知识点
21.
正确答案
略
解析
解析已在路上飞奔,马上就到!
知识点
22.已知













(1)写出


(2)证明




(3)设点

正确答案
(3)假设有两个点


即
所以

消去


以下考查数列

当

所以对于数列
∴不可能存在

解析
解析已在路上飞奔,马上就到!