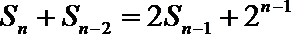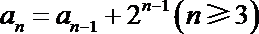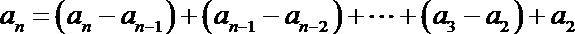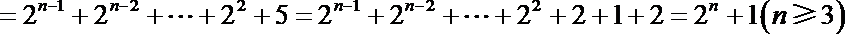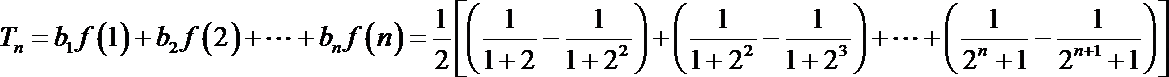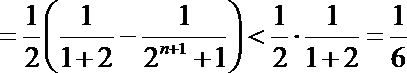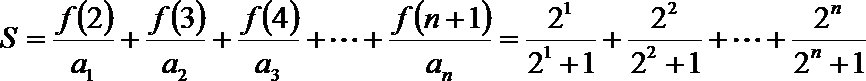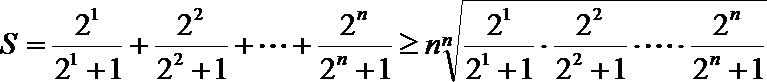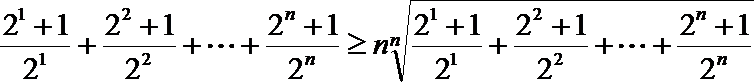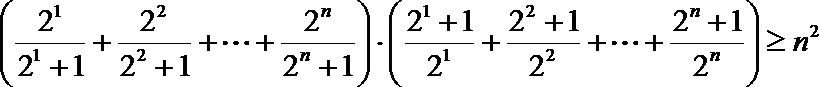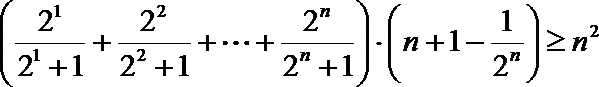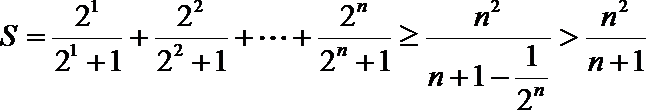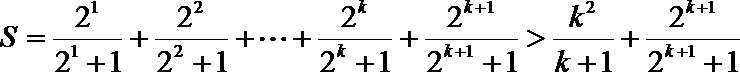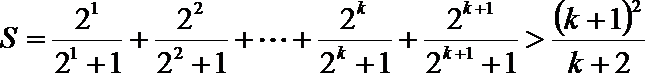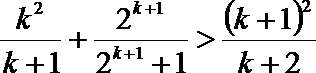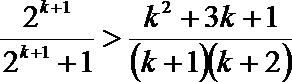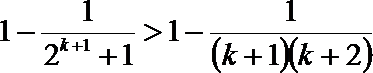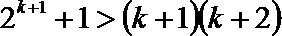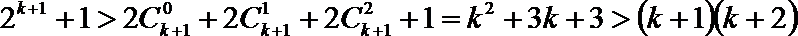1.已知复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若正数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.以抛物线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 设m、n是两条不同的直线,
①


②
③
④
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.陈、余两家夫妇二人各带1个小孩一起去参观园博园,购票后排队依次入园。为安全起见,首尾一定要排两位爸爸,另外,两位小孩一定要排在一起,则这6人的入园顺序排法种数共有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图如图所示,现规定不低于70分为合格,则合格人数是__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.椭圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若


正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 如图,球







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设函数
(1)求函数
(2)设





正确答案
解:
(1)
所以当



故函数
(2) 由

又
由
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,已知四棱锥










(1)求证:

(2)求二面角
正确答案
(1)证明:取SC的中点R,连QR, DR.. 由题意知:PD∥BC且PD=





(2)
法一:

法二:以P为坐标原点,PA为x轴,PB为y轴,PS为z轴建立空间直角坐标系,则S(



面PBC的法向量为


由
cos
解析
解析已在路上飞奔,马上就到!
知识点
17.四川灾后重建工程督导评估小组五名专家被随机分配到A、B、C、D四所不同的学校进行重建评估工作,要求每所学校至少有一名专家。
(1)求评估小组中甲、乙两名专家不在同一所学校的概率;
(2)设随机变量


正确答案
解:
(1)记评估小组中甲、乙两名专家被分配在同一所学校的事件为F,那么P(F)=
所以甲、乙两名专家不在同一所学校的概率为:P(

(2)随机变量


P(

所以
所以



解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(I)当

(II)若函数





正确答案
解:
(I)当

令


令


(II)因为函数

所以
所以



函数

所以只需
解得
解析
解析已在路上飞奔,马上就到!
知识点
20.已知点F是抛物线C:

(1)求点S的坐标;
(2)以S为圆心的动圆与
①判断直线MN的斜率是否为定值,并说明理由;
②延长NM交

正确答案
解:
(1)设



∴
(2)
①设直线SA的方程为

∴
由已知SA=SB,∴直线SB的斜率为

∴
②设E(t,0),∵|EM|=




∴直线SA的方程为

∴
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列

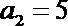
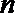
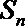
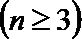
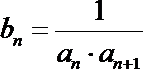
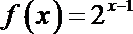
(1)求数列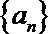
(2)求证: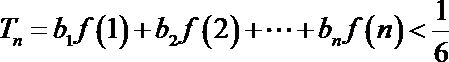
(3)求证: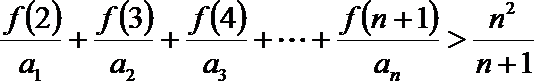
正确答案
(1)由题意知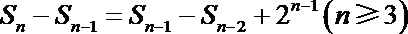
∴
检验知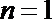
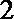
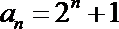
(2)
(3)
法一:令
两式相乘有
法二:可用柯西不等式
法三:数学归纳法:
①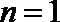
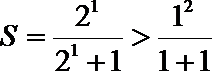
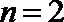
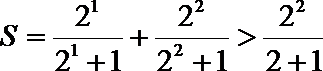
(只写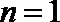
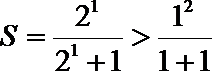
②假设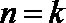
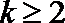
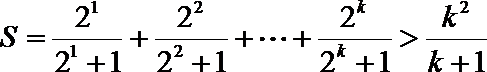
则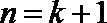
要证
只需证
即证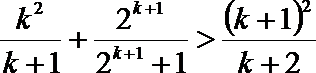
即证
即证
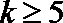
再验证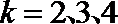
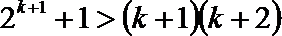
解析
解析已在路上飞奔,马上就到!