2.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=1,b=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若函数
正确答案
0≤a≤1
解析
解析已在路上飞奔,马上就到!
知识点
7.一个正四棱柱的各个顶点在一个直径为2cm的球面上.如果正四棱柱的底面边长为1cm,那么该棱柱的表面积为________cm2.
正确答案
2+4
解析
解析已在路上飞奔,马上就到!
知识点
8.已知双曲线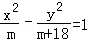
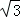
正确答案
±24
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数y=f(x)的图象与函数y=ax(a>0且a≠1)的图象关于直线y=x对称,记g(x)=f(x)[f(x)+2f(2)﹣1].若y=g(x)在区间[
正确答案
(0,
解析
解析已在路上飞奔,马上就到!
知识点
1.设P和Q是两个集合,定义集合P﹣Q={x|x∈P,且x∉Q},如果P={x|log2x<1},Q={x||x﹣2|<1},那么P﹣Q等于________.
正确答案
(0,1]
解析
解析已在路上飞奔,马上就到!
知识点
3.若数列{an}满足:a1=1,an+1=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若(x2+

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
6.在数列{an}中,若a1=1,an+1=2an+3(n≥1),则该数列的通项an=________.
正确答案
2n+1﹣3
解析
解析已在路上飞奔,马上就到!
知识点
9.如图,平面内有三个向量













正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
14.设函数f(x)=x2+1,若关于x的不等式f(

正确答案
(﹣∞,﹣

解析
解析已在路上飞奔,马上就到!
知识点
15.在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”,类似的,我们在平面向量集D={





①若





②若





③若






④对于任意向量








其中真命题的序号为________.
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
11.已知⊙O的方程是x2+y2﹣2=0,⊙O'的方程是x2+y2﹣8x+10=0,由动点P向⊙O和⊙O'所引的切线长相等,则动点P的轨迹方程是________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.从4名男同学和3名女同学中随机选出3人参加演讲比赛,则女同学被抽到的数学期望为________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知实数x、y满足
正确答案
[- 5,7]
解析
解析已在路上飞奔,马上就到!
知识点
17.下列各小题中,p是q的充分必要条件的是()
①p:m<﹣2,或m>6;q:x2+mx+m+3有两个不同的零点;
②p:
③p:cosα=cosβ;q:tanα=tanβ;
④p:A∩B=A;q:∁UB⊆∁UA.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知满足条件x2+y2≤1的点(x,y)构成的平面区域面积为S1,满足条件[x]2+[y]2≤1的点(x,y)构成的平面区域的面积为S2,其中[x]、[y]分别表示不大于x,y的最大整数,例如:[﹣0.4]=﹣1,[1.6]=1,则S1与S2的关系是()
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,动点P在正方体ABCD﹣A1B1C1D1的对角线BD1上.过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,N.设BP=x,MN=y,则函数y=f(x)的图象大致是()
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知△ABC三个顶点的直角坐标分别为A(3,4)、B(0,0)、C(c,0).
(1)若
(2)若c=5,求sinA的值.
正确答案
(1)由A(3,4)、B(0,0)、C(c,0).
得到:

则

解得c=
(2)当c=5时,C(5,0),
则|AB|=
|AC|=

根据余弦定理得:
cosA=


由A∈(0,π),
得到sinA=

解析
解析已在路上飞奔,马上就到!
知识点
23.对于定义在R上的函数f(x),可以证明点A(m,n)是f(x)图象的一个对称点的充要条件是f(m﹣x)+f(m+x)=2n,x∈R.
(1)求函数f(x)=x3+3x2图象的一个对称点;
(2)函数f(x)=ax3+(b﹣2)x2(a,b∈R)在R上是奇函数,求a,b满足的条件;并讨论在区间[﹣1,1]上是否存在常数a,使得f(x)≥﹣x2+4x﹣2恒成立?
(3)试写出函数y=f(x)的图象关于直线X=M对称的充要条件(不用证明);利用所学知识,研究函数f(x)=ax3+bx2(a,b∈R)图象的对称性。
正确答案
(1)解:设A(m,n)为函数f(x)=x3+3x2图象的一个对称点,
则f(m﹣x)+f(m+x)=2n,对于x∈R恒成立.
即(m﹣x)3+3(m﹣x)2+(m+x)3+3(m+x)2=2n对于x∈R恒成立,
∴(6m+6)x2+(2m3+6m2﹣2n)=0由
解得:
故函数f(x)图象的一个对称点为(﹣1,2).
(2)①因为函数是奇函数,则由f(﹣x)=﹣f(x)
得:﹣ax3+(b﹣2)x2=﹣ax3﹣(b﹣2)x2,
解得a∈R,b=2;
②当a∈R,b=2时f(x)是奇函数.不存在常数a使f(x)≥﹣x2+4x﹣2x∈[﹣1,1]时恒成立.
依题,此时f(x)=ax3,
令g(x)=﹣x2+4x﹣2,x∈[﹣1,1],
∴g(x)∈[﹣7,1],
若a=0,f(x)=0,不合题;
若a>0,f(x)=ax3此时为单调增函数,f(x)min=﹣a.
若存在a合题,则﹣a≥1,与a>0矛盾.
若a<0,f(x)=ax3此时为单调减函数,
f(x)min=a若存在a合题,则a≥1,与a<0矛盾.
综上可知,符合条件的a不存在.
(3)函数的图象关于直线x=m对称的充要条件是f(m+x)=f(m﹣x)
①a=b=0时,f(x)=0(x∈R),其图象关于x轴上任意一点成中心对称;关于平行于y轴的任意一条直线成轴对称图形;
②a=0,b≠0时,f(x)=bx2(x∈R),其图象关于y轴对称图形;
③a≠0,b=0时,f(x)=ax3,其图象关于原点中心对称;
④a≠0,b≠0时,f(x)=ax3+bx2的图象不可能是轴对称图形.
设A(m,n)为函数f(x)=ax3+bx2图象的一个对称点,
则f(m﹣x)+f(m+x)=2n对于x∈R恒成立.
即a(m﹣x)3+b(m﹣x)2+a(m+x)3+b(m+x)2=2n对于x∈R恒成立,(3am+b)x2+(am3+bm2﹣n)=0
,由
故函数f(x)图象的一个对称点为(﹣

解析
解析已在路上飞奔,马上就到!
知识点
21.如图,在四棱锥P﹣ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
(1)求证:PB⊥DM;
(2)求CD与平面ADMN所成的角.
正确答案
(1)因为N是PB的中点,PA=AB,
所以AN⊥PB.
因为AD⊥平面PAB,所以AD⊥PB,
从而PB⊥平面ADMN.
因为DM⊂平面ADMN,
所以PB⊥DM.
(2)取AD的中点G,连接BG、NG,
则BG∥CD,
所以BG与平面ADMN所成的角和CD与平面ADMN所成的角相等.
因为PB⊥平面ADMN,
所以∠BGN是BG与平面ADMN所成的角.
在Rt△BGN中,
故CD与平面ADMN所成的角是
解析
解析已在路上飞奔,马上就到!
知识点
22.在m(m≥2)个不同数的排列P1P2…Pn中,若1≤i<j≤m时Pi>Pj(即前面某数大于后面某数),则称Pi与Pj构成一个逆序.一个排列的全部逆序的总数称为该排列的逆序数.记排列(n+1)n(n﹣1)…321的逆序数为an,如排列21的逆序数a1=1,排列321的逆序数a3=6.
(1)求a4、a5,并写出an的表达式;
(2)令
正确答案
(1)由排列21的逆序数a1=1,排列321的逆序数a2=3,排列4321的逆序数a3=6,
得a4=4+3+2+1=10,a5=5+4+3+2+1=15,所以an=n+(n﹣1)+…+2+1=
(2)因为
所以b1+b2+…+bn>2n.
又因为
所以b1+b2+…+bn=2n+2[(



综上,2n<b1+b2+bn<2n+3,n=1,2,…
解析
解析已在路上飞奔,马上就到!
知识点
24.在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为DAB=|x1﹣x2|+|y1﹣y2|.
(1)在平面直角坐标系中,写出所有满足到原点的直角距离为2的“格点”的坐标(“格点”指的是横、纵坐标均为整数的点)
(2)求到两定点F1、F2的“直角距离”之和为定值2a(a>0)的动点的轨迹方程,并在直角坐标系内作出该动点的轨迹;
①F1(﹣1,0)、F2(1,0)、a=2;
②F1(﹣1,﹣1)、F2(1,1)、a=2
③F1(﹣1,﹣1)、F2(1,1)、a=4;
(3)写出同时满足以下两个条件的所有格点的坐标,并说明理由;
①到A(﹣1,﹣1)、B(1,1)两点的“直角距离”相等;
②到C(﹣2,﹣2)、D(2,2)两点的“直角距离”之和最小。
正确答案
(1)设点P(x,y),则有新定义可得,|x|+|y|=2,
则满足条件的格点的坐标为(0,2),(0,﹣2),(1,1),(1,﹣1),(﹣1,1),(﹣1,﹣1),(2,0),(﹣2,0);
(2)①动点的轨迹方程为|x+1|+|x﹣1|+2|y|=4,如图1所示轨迹为六边形.
②|x+1|+|x﹣1|+|y﹣1|+|y+1|=4,如图2所示轨迹为正方形及内部.
③|x+1|+|x﹣1|+|y﹣1|+|y+1|=8,如图3所示轨迹是八边形.
(3)设满足条件的格点的坐标为(x,y),
则由①,得|x+1|+|y+1|=|x﹣1|+|y﹣1|,当x≥1,y≥1,x+y+2=x+y﹣2不成立;
当x≤﹣1,y≤﹣1,方程也不成立;
当x≥1,y≤﹣1,x+1﹣y﹣1=x﹣1+1﹣y成立;
当x≤﹣1,y≥1,也成立;
当x≥1,﹣1<y<1,x+1+y+1=x﹣1+1﹣y,则y=﹣1;
当x≤﹣1,﹣1<y<1,则y=1;
当﹣1<x<1,y≥1,x+1+y+1=1﹣x+y+1,则x=0;
当﹣1<x<1,y≤﹣1,x+1﹣y﹣1=1﹣x+1﹣y,则x=1;
当﹣1<x<1,﹣1<y<1,x+1+y+1=1﹣x+1﹣y,则x+y=0.
由②得,到C(﹣2,﹣2)、D(2,2)两点的“直角距离”之和d=|x+2|+|x﹣2|+|y+2|+|y﹣2|≥|(2+x)+(2﹣x)|+|(2+y)+(2﹣y)=4+4=8,当且仅当﹣2≤x≤2且﹣2≤y≤2,取得最小值8.
综合上面,可得格点为(2,﹣1),(2,﹣2),(1,﹣1),(1,﹣2),(0,0),(﹣1,2),(﹣1,1),(﹣2,2),(﹣2,1).
解析
解析已在路上飞奔,马上就到!























