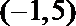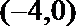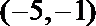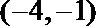3.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若n<0,m>0,且m+n>0,则下列不等式中成立的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.“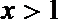

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知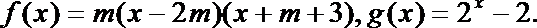
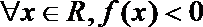
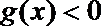

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在R上定义运算⊙:a⊙b=ab+2a+b,则满足x⊙(x-2)<0的实数x的取值范围为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若变量x,y满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.某公司生产甲、乙两种桶装产品,已知生产甲产品1桶需耗A原料1千克、B原料2千克;生产乙产品1桶需耗A原料2千克,B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知x、y满足以下约束条件
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.下列命题为真的是______。
①
②
③
④当x≥2时,
⑤当0<x≤2时,
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
14.己知不等式ax2-5x+b>0的解集是{x|-3<x<-2},则不等式bx2-5x+a<0的解集是____________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
16.已知x、y满足不等式组
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少要含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
正确答案
设为该儿童分别预订

设费用为

由题意知:

画出可行域如图:
变换目标函数:
这是斜率为



当截距

由图知当目标函数过点
即直线


z取到最小值,即要满足营养要求,并且花费最少,
应当为该儿童分别预订4个单位的午餐和3个单位的晚餐
解析
解析已在路上飞奔,马上就到!
知识点
18.设命题P:关于x的不等式a

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知



正确答案
∵
∴
∵


∴
解析
解析已在路上飞奔,马上就到!
知识点
20.已知不等式
(1)求
(2)解不等式
正确答案
(1)
(2)


解析
解析已在路上飞奔,马上就到!
知识点
21.某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元。该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨。问该企业如何安排可获得最大利润,最大利润是多少?
正确答案
设生产甲产品

则有:
目标函数
作出可行域(如图)
平移直线
故生产甲产品3吨,生产乙产品4吨时,可获得最大利润为27万元。
解析
解析已在路上飞奔,马上就到!
知识点
22.设不等式




正确答案
因为
所以
所以
解析
解析已在路上飞奔,马上就到!