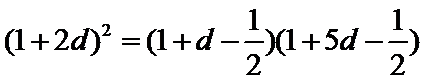1.已知

正确答案
解析

考查方向
解题思路
从内到外依次求值。
易错点
计算粗心出错。
知识点
2.若直线



正确答案
解析
由向量共线的定义可知,两直线平行可以得到
考查方向
解题思路
分别判断。
易错点
判断出错。
知识点



正确答案
解析
求出x的平均值为2,设看不清的数为k,则y的平均值为

考查方向
解题思路
根据回归直线方程过样本的中心点即可。
易错点
不记得相关知识点。
知识点
5. 函数
正确答案
解析
令


考查方向
解题思路
可以用换元法解。
易错点
粗心计算出错。
知识点
6.函数
正确答案
解析






考查方向
解题思路
先求出定义域,再求出内函数的增区间。
易错点
不再定义域内去求。
知识点
7.若一个双曲线实轴的长度、虚轴的长度和焦距依次成等差数列,则该双曲线的离心率是( )
正确答案
解析
由已知可得2a+2c=2b,即a+c=b,左右同时平方再将

考查方向
解题思路
由已知构造一个方程即可解出。
易错点
粗心计算出错。
知识点
9.已知





正确答案
解析
A区域的面积是4,而B在A中的面积为



考查方向
解题思路
转化为面积之比来解答。
易错点
不会画示意图。
知识点
4.若两个正实数



正确答案
解析
不等式




考查方向
解题思路
不等式
易错点
不会转化。
知识点
8.在



正确答案
解析
由




考查方向
解题思路
先算出角B的余弦值,在用余弦定理计算AC.
易错点
夹角搞错。
知识点
10.数列



正确答案
解析
由已知





考查方向
解题思路
找出规律,再利用周期性来解答。
易错点
不能找到规律。
知识点
12.已知函数

正确答案
解析
由题意可知只有满足a>0且满足



考查方向
解题思路
根据函数的图像有3个交点来解答。
易错点
不会做。
知识点
11.将正方体(如图1所示)截去两个三棱锥,得到如图2所示的几何体,则该几何体的左视图为( )
正确答案
B
解析
由图像可以直接判断,挡住的部分是虚线,所以选B.
考查方向
解题思路
直接由图像判断。
易错点
缺乏空间想象力。
知识点
13.若



正确答案
解析
由判别式小于等于0,即实数

考查方向
解题思路
直接由判别式小于等于0即可。
易错点
不会转化。
知识点

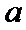

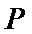
正确答案
4
解析
由已知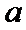
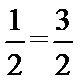
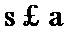
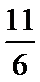
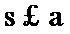
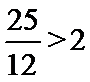

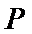
考查方向
解题思路
按照框图的顺序直接计算即可。
易错点
粗心出错。
知识点
15.已知直线






正确答案
解析
由已知可知直线过定点(2,3),又已知圆的圆心坐标为(1,2),所以所求直线必过点(2,3),且与过这两点(2,3),(1,2)所在的直线垂直,故可解得弦

考查方向
解题思路
找出所过的定点,然后再去求直线的方程。
易错点
不会将已知转化为所学内容去做。
知识点
16.
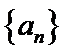
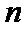
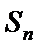
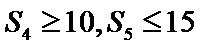
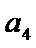
正确答案
4
解析
由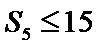
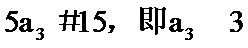
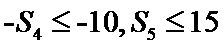
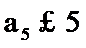
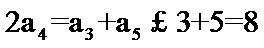
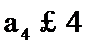
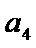
考查方向
解题思路
根据已知条件最后求出要求的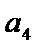
易错点
已知条件不会转化。
知识点
已知等差数列


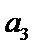
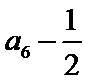
17.求
18.设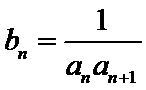
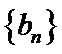

正确答案
(1)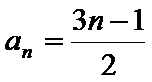
解析
试题分析:本题属查了等差和等比数列及裂项相消法求和,(1)根据已知条件构造方程解出公差d,再求出通项公式;(2)利用裂项相消法求解。
(I)由题意设
得

考查方向
解题思路
本题考查了等差和等比数列及裂项相消法求和,解题步骤如下:(1)根据已知条件构造方程解出公差d,再求出通项公式;(2)利用裂项相消法求解。
易错点
不会利用裂项相消法解题。
正确答案
(2)
解析
试题分析:本题属查了等差和等比数列及裂项相消法求和,(1)根据已知条件构造方程解出公差d,再求出通项公式;(2)利用裂项相消法求解。
(II)
考查方向
解题思路
本题考查了等差和等比数列及裂项相消法求和,解题步骤如下:(1)根据已知条件构造方程解出公差d,再求出通项公式;(2)利用裂项相消法求解。
易错点
不会利用裂项相消法解题。
19.某班
(Ⅰ)求

(Ⅱ)数学老师决定从第一组和第五组的学生中随机抽取2名进行交流,求第一组至少有一名学生被抽到的概率;
(III)设从第一组或第五组中任意抽取的两名学生的数学测试成绩分别记为

正确答案
(1)


解析
试题分析:本题属频率分布表和古典概型,(1)直接按照步骤来求,根据频率相加等于1;(2)利用古典概型公式来计算;(3)利用古典概型公式来计算.
(Ⅰ)

(Ⅱ)设第5组的3名学生分别为

则从5名学生中抽取两位学生有:
其中第一组的2位学生

所以第一组至少有一名学生被老师抽到的概率为
(III)第1组





使

所以


考查方向
解题思路
本题考频率分布表和古典概型,解题步骤如下:(1)直接按照步骤来求,根据频率相加等于1;(2)利用古典概型公式来计算;(3)利用古典概型公式来计算。
易错点
列举事件的时候容易重复或者遗漏。
知识点
如图,










20.求证:平面

21.设几何体




正确答案
(1)见解析;
解析
试题分析:本题属立体几何证明与体积的计算问题,题目的难度是逐渐由易到难,(1)利用面面垂直的判定定理来证明;(2)将体积表示出来再计算其比值。
(Ⅰ)证明:如图.




平面







又









【注】也可证明

考查方向
解题思路
本题考立体几何证明与体积的计算问题,解题步骤如下:(1)利用面面垂直的判定定理来证明;(2)将体积表示出来再计算其比值。
易错点
定理使用条件不全。
正确答案
(2)
解析
试题分析:本题属立体几何证明与体积的计算问题,题目的难度是逐渐由易到难,(1)利用面面垂直的判定定理来证明;(2)将体积表示出来再计算其比值。
(Ⅱ)几何体

过点








则

因此,
考查方向
解题思路
本题考立体几何证明与体积的计算问题,解题步骤如下:(1)利用面面垂直的判定定理来证明;(2)将体积表示出来再计算其比值。
易错点
定理使用条件不全。
已知椭圆

22.求椭圆E的方程;
23.设经过

正确答案
(1)
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)待定系数法解;(2)用设而不求的方法来解答。
(I)设椭圆E:
考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)待定系数法解;(2)用设而不求的方法来解答。
易错点
计算量大,计算不出来。
正确答案
(2)x=4
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)待定系数法解;(2)用设而不求的方法来解答。
(II)将直线



直线AM的方程为

直线BN的方程为

联立得
或

考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)待定系数法解;(2)用设而不求的方法来解答。
易错点
计算量大,计算不出来。
如图,








26.求
27.求证:
正确答案
(1)
解析
试题分析:本题属几何证明选讲中的切割线定理及相交弦定理,(1)直接按照步骤来求(2)要注意对参数的讨论(3)涉及恒成立问题,转化成求函数的最值,
(Ⅰ)由切割线定理知:



考查方向
解题思路
本题考几何证明选讲中的切割线定理及相交弦定理,解题步骤如下:(1)
利用切割线定理及三角形相似即可解出;(2)利用第一问及结合相交弦定理即可证明。
易错点
定理的使用不熟练。
正确答案
(2)见解析。
解析
试题分析:本题属几何证明选讲中的切割线定理及相交弦定理,(1)直接按照步骤来求(2)要注意对参数的讨论(3)涉及恒成立问题,转化成求函数的最值,
(Ⅱ)

考查方向
解题思路
本题考几何证明选讲中的切割线定理及相交弦定理,解题步骤如下:(1)
利用切割线定理及三角形相似即可解出;(2)利用第一问及结合相交弦定理即可证明。
易错点
定理的使用不熟练。
已知函数
24.当

25.当




正确答案
(1)


解析
试题分析:本题属函数与导数,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)利用导数这个工具来解答即可。
(Ⅰ)
所以


考查方向
解题思路
本题考函数与导数,解题步骤如下:(1)直接按照步骤来求;(2)利用导数这个工具来解答即可。
易错点
第二问计算不出来。
正确答案
(2)
解析
试题分析:本题属函数与导数,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)利用导数这个工具来解答即可。
(Ⅱ)
设t=
又


考查方向
解题思路
本题考函数与导数,解题步骤如下:(1)直接按照步骤来求;(2)利用导数这个工具来解答即可。
易错点
第二问计算不出来。