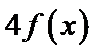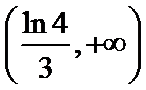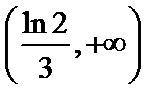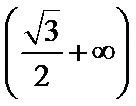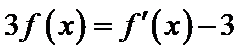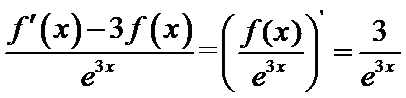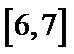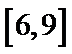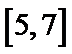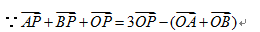1.已知复数
正确答案
解析


考查方向
解题思路
本题属于简单题,可使用直接法,
(1)化简z得到
(2)观察实部和虚部对应的正负
易错点
计算过程易忽略
知识点
2.已知集合


正确答案
解析

考查方向
解题思路
本题属于简单题,可使用直接法,
(1)分别求解不等式,
(2)确定交集运算
易错点
计算过程对一元二次不等式出错,对对数函数的单调性判断错误,不能区分交并概念
知识点
7.函数

正确答案
解析
由题意可知T=



考查方向
解题思路
1、利用相邻的零点与对称轴之间的距离求出


易错点
本题易于在求解
知识点
10.设函数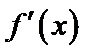

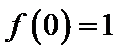
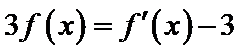
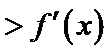
正确答案
解析
:有题意知导函数于原函数之间没有用变量x联系,可知函数与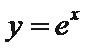
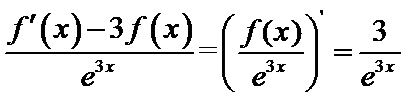
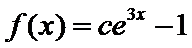
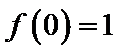
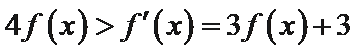
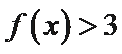
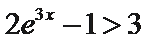

考查方向
解题思路
该题隐含突破点在于
1构造
2根据定积分得原函数函数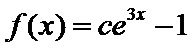
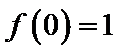
3解指数不等式得出结果
易错点
本题易错于函数的构造过程,
知识点
3.某校高一、高二、高三年级学生人数分别是400,320,280.采用分层抽样的方法抽取50人,参加学校举行的社会主义核心价值观知识竞赛,则样本中高三年级的人数是( )
正确答案
解析
高三年级的人数是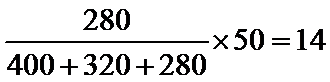
考查方向
解题思路
根据分层抽样的性质,首先求出高三年级在三个年级中所占有的比例,
易错点
主要是数据较大计算错误
知识点
4.已知命题


正确答案
解析







考查方向
解题思路
该题解答需要这么几步:①对P,q真假的判断,②且或非命题真假判断
易错点
①忽视存在性命题和全称命题的含义,②且或非真假判断
知识点
5.已知x,y满足约束条件
正确答案
解析
方法1:线性规划问题中最优解出现在可行域的顶点上,因为有三个约束条件,所以顶点即三条直线的交点(两两结合解方程组)A(1,1), B(1,5), C(-3,-3),依次带入判断出答案A,
该方法缺点是只能解决三条直线的问题,超过三条需要判断那些点是在可行域上
方法2:画出可行域如图
考查方向
解题思路
该题有两个解法,方法一:线性规划问题中最优解出现在可行域的顶点上,因为有三个约束条件,所以顶点即三条直线的交点,一一求解验证
方法二,根据条件画出可行域,平移直线3x-2y=0,找出最优解,
易错点
主要体现在两个方面①可行域不规范,②直线平移过程忽略直线的斜率
知识点
6.某几何体的三视图如图所示,则该几何体的体积是( )
正确答案
解析
作为选择题,可以使用第一种方法:根据三视图可以得到该几何体为三棱锥,所以可以确定计算的体积公式
考查方向
解题思路
本题主要可以从两个方面考虑,第一个直观图与三视图之间的关系,通过这个关系直接读取直观图的形状,及其相关数据,进而计算,第二就是画出直观图,利用三视图相关数据标记直观图的数据,再进一步利用常见几何体的体积公式计算
易错点
主要出现在两个地方:①三视图还原直观图错误,②直观图读取直观图数据错误,特别是底面上的长宽数据
知识点
8.公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )
(参考数据:

正确答案
解析
n=6,s=
n=12,s=3
n=24,s=3.1056
输出n=24
考查方向
解题思路
该题首先根据选项得出是带入验证问题,这是该题的切入点,可以极大的简化解题过程,简单说就是带值检验
易错点
本题易在判断上出错,导致提前或者延后跳出循环,第二找不出循环次数与n之间的关系,导致出错,三、三角计算出错,导致结果出错
知识点
9.在平面直角坐标系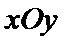
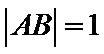
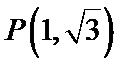
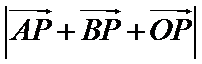
正确答案
解析
考查方向
解题思路
使用向量的几何意义,
易错点
本题易错于几何意义的转换,或者在使用坐标化的过程中A,B两点的形成过程,代数法构建过程繁琐,学生易计算出错,
知识点
11.二项式
正确答案
20
解析




考查方向
解题思路
写出二项展开式,确定r,直接计算
易错点
本题易错在二项展开式记忆错误
知识点
13.已知等比数列


正确答案
2
解析
考查方向
解题思路
该题思路比较简单直接
易错点
本题注意定积分计算易出错,公比求的两个结果都保留
知识点
12.已知向量



正确答案
解析
考查方向
解题思路
本题主要是突破点在于垂直与数量积之间的转换
易错点
本题注意向量垂直与数量积之间的转换
知识点
14.过点

正确答案
3
解析
考查方向
解题思路
该题思路比较清晰,主要有以下几个步骤
易错点
本题易错点主要集中在,1、渐近线的表达,2、曲线上点的问题转化为两直线之间的距离问题
知识点
15.已知函数

正确答案
解析
考查方向
解题思路
该题信息量比较大关键在于理清解题思路
易错点
本题易错点有:1、图像画不出,2、关于
知识点
18.求证:DE//面PAB
19.求二面角
正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
16.求角C的值
17.若



正确答案
解析
考查方向
解题思路
该题解题思路如下
易错点
该题对于三角形中的角的关系出错,和角公式展开化简计算错误
正确答案
解析
考查方向
解题思路
该题解题思路如下
易错点
该题对于三角形中的角的关系出错,和角公式展开化简计算错误
20.求选手甲第一关闯关成功且所得学豆为零的概率;
21.设该选手所得学豆总数为X,求X的分布列与数学期望.
正确答案
见解析
解析
考查方向
解题思路
本题的解题思路
易错点
本题第一问在情况分析上容易遗漏,第二问可能取值考虑不全
正确答案
见解析
解析
考查方向
解题思路
本题的解题思路
易错点
本题第一问在情况分析上容易遗漏,第二问可能取值考虑不全
22.求数列

23.令



正确答案
见解析
解析
考查方向
易错点
本题第一问忽略


正确答案
见解析
解析
考查方向
易错点
本题第一问忽略


已知函数
24.当a=1,求函数
25.当a<0,且对任意实数

正确答案
见解析
解析
函数

当







考查方向
解题思路
该题的突破点在意恒成立的巧妙转换为最值问题
易错点
本题易错在简单函数符合函数求导,恒成立问题的转化不清,函数分类讨论不清,
正确答案
见解析
解析
令



由于
当




所以
当




当


(i)当








(ii) 当






只需

(iii) 当






综上所述,
考查方向
解题思路
分别求

易错点
本题易错在简单函数符合函数求导,恒成立问题的转化不清,函数分类讨论不清,
设椭圆


26.求椭圆C的方程和“相关圆”E的方程;
27.过“相关圆”E上任意一点P作“相关圆”E的切线l与椭圆C交于A,B两点,O为坐标原点。证明:∠AOB为定值
29.连接PO并延长交“相交圆”E于点Q,求△ABQ面积的取值范围.
正确答案
见解析
解析
解:因为若抛物线


又因为椭圆
故椭圆

“相关圆”
考查方向
解题思路
利用圆锥曲线的定义和性质求解曲线方程
易错点
本题主要有以下几个错误:1、抛物线焦点求措,2、无法确确定定值,进而无法确定解题过程,3、求△ABQ面积无法确定底和高
正确答案
见解析
解析
解: (i)当直线

则
当直线

联立方程组


△=
因为直线与相关圆相切,所以


考查方向
解题思路
利用特殊位置求定值,一般位置去证明的思想,先确定k不存在时的角的取值即为定值,
易错点
本题主要有以下几个错误:1、抛物线焦点求措,2、无法确确定定值,进而无法确定解题过程,3、求△ABQ面积无法确定底和高
正确答案
见解析
解析
解:由于



当直线AB的斜率不存在时,由(i)知
因为

① 



所以
当且仅当
②当


考查方向
解题思路
明确高已知,求解直线和圆的交点弦的长构造均值定理求解取值范围
易错点
本题主要有以下几个错误:1、抛物线焦点求措,2、无法确确定定值,进而无法确定解题过程,3、求△ABQ面积无法确定底和高