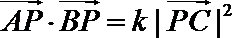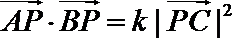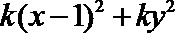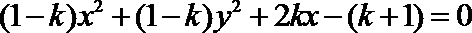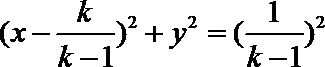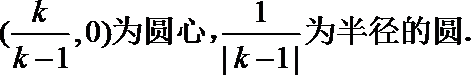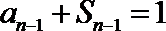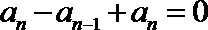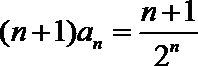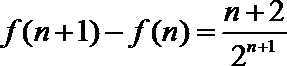2.计算
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知




正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
7.三阶行列式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下边的程序框图(如图所示),能判断任意输入的整数x是奇数或是偶数.其中判断框内的条件是__________
正确答案
m=0
解析
解析已在路上飞奔,马上就到!
知识点
1. 计算
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.直线ax+3y+4=0与直线2x+(a+1)y+1=0平行,则实数a的值是_____.
正确答案
-3或2
解析
解析已在路上飞奔,马上就到!
知识点
6.已知直线
正确答案
0或
解析
解析已在路上飞奔,马上就到!
知识点
9.已知n次多项式



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.过点

正确答案
x+y-2=0
解析
解析已在路上飞奔,马上就到!
知识点
11.受2008年国际金融危机的影响,某企业单位在人事制度改革中对员工进行分流,被分流的入员当年可在原单位领取原工资的100%,从第二年起每年只在原单位领取前一年工资的



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
12.用向量方法可以证明:若P为正三角形内切圆上任意一点,则点P到三角形三个顶点距离的平方和为定值.请你针对这个问题进行研究,写出一个推广后的正确命题:______________________.
正确答案
①若P为正三角形外接圆上任意一点,则点P到三角形三个顶点距离的平方和为定值.
②若正三角形




③若P为正多边形内切圆上任意一点,则点P到各个顶点距离的平方和为定值.
④若P为正多边形外接圆上任意一点,则点P到各个顶点距离的平方和为定值.
解析
解析已在路上飞奔,马上就到!
知识点
19.已知定点A(0,1),B(0,-1),C(1,0),动点P满足:
(1)求动点P的轨迹方程,并说明方程表示的曲线类型;
(2)求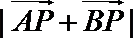
正确答案
(1)设动点P(x,y),
则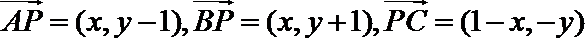
由
得x2+y2-1=
化简得
当k=1时,方程为x=1,表示直线;
当k≠1时,方程为
表示以
(2)当k=2时,点P的轨迹方程为
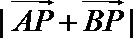
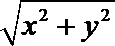

所以2≤
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量



(1)求直线l的方程;
(2)当直线l被圆C截得的弦长为
正确答案
(1)
所以,直线l的点方向式方程为
(2)又题意
解得m=
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列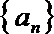
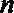
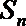
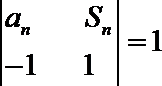
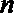
(1)求数列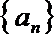
(2)记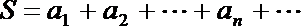

正确答案
(1)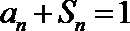
以上两式相减得到
即
所以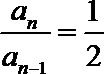
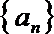

又

所以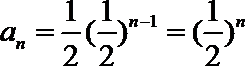
(2)
设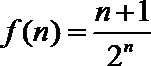
则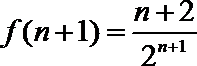
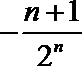
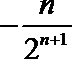
所以,函数f(n)在n∈N*上单调递减,
所以f(n)的最大值是f(1)=1,
所以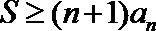
解析
解析已在路上飞奔,马上就到!
知识点
20.在平面直角坐标系中,已知三个点列





(1)证明:数列
(2)试用


(3)设





(4)若

正确答案
(1)因为点列
所以

所以数列
(2) 

因为
所以
又





将以上等式相加得
所以
(3)
若存在这样的实数



则

(4)
由

即
记

解得n≥4或n≤1,但由于n≥2,所以n≥4,kmin=4.
解析
解析已在路上飞奔,马上就到!
知识点
13.设凸k边形的内角和为f(k),则凸k+1边形的内角和f(k+1)=f(k)+( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.如图所示的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵列成等比数列,则实数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.经济学中的“蛛网理论”(如图),假定某种商品的“需求—价格”函数的图象为直线l1,“供给—价格”函数的图象为直线l2,它们的斜率分别为k1.k2,l1与l2的交点P为“供给—需求”均衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点P,与直线l1. l2的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点P的条件为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!