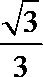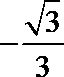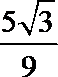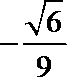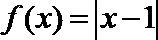2.在复平面内，复数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4.已知函数
A关于点
B关于直线
C向左平移
D向左平移
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.若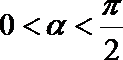
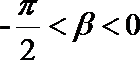
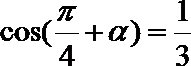
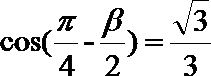
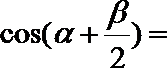
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5.过椭圆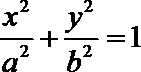
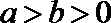
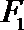
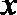
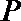
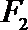
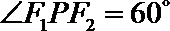
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3.函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6.由等式
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8.在△ABC中，AB=4，∠ABC=30°，D是边
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1.若全集为实数集
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7.已知A，B，C，D是函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10.若在区域
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12.设函数
A13
B5
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11.已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19.已知函数
（1）实数m的取值集合为A，当m取集合A中的最小值时，定义数列
（2）若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17.在△ABC中，a，b，c分别是角A，B，C的对边长，已知
（Ⅰ）求cosB及tan
（Ⅱ）若b＝2
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
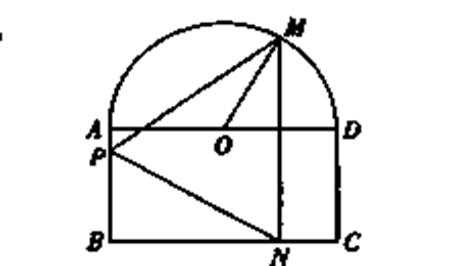
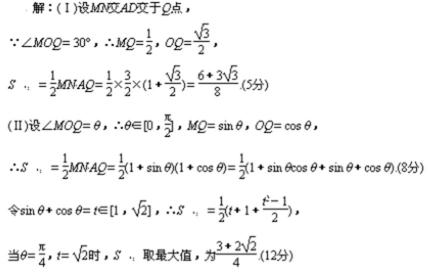
20.如图，一个半圆和长方形组成的铁皮，长方形的边AD为半圆的直径，O为半圆的圆心，AB＝1，BC＝2，现要将此铁皮剪出一个等腰三角形PMN，其底边MN⊥BC．
（Ⅰ）设∠MOD＝30°,求三角形铁皮PMN的面积；
（Ⅱ）求剪下的铁皮三角形PMN的最大面积
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18.如图，从A1（1,0,0），A2（2,0,0），B1（0,1,0,）B2（0,2,0），C1（0,0,1），C2（0,0,2）这6个点中随机选取3个点。
（1）求这3点与原点O恰好是正三棱锥的四个顶点的概率；
（2）求这3点与原点O共面的概率。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21.已知函数f(x)＝－x3＋x2－2x(a∈R)．
（1）当a＝3时，求函数f(x)的单调区间；
（2）若对于任意x∈[1，＋∞)都有f′(x)<2(a－1)成立，求实数a的取值范围；
（3）若过点可作函数y＝f(x)图象的三条不同切线，求实数a的取值范围．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
请在第22、23两题中任选一题作答
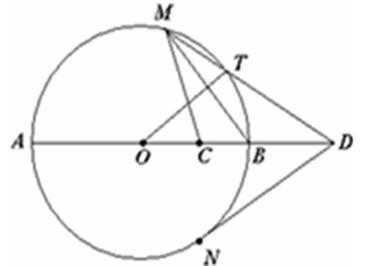
22.如图，AB是圆O的直径，C是半径OB的中点， D是OB延长线上一点，且BD=OB，直线MD与圆O相交于点M、T（不与A、B重合），DN与圆O相切于点N，连结MC，MB，OT．
（I）求证：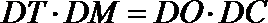
（II） 若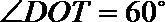
23.已知函数
（I）解不等式: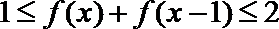 
（II）若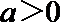
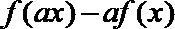
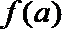
正确答案
22.
23.
解析
解析已在路上飞奔，马上就到！
知识点
13.已知倾斜角为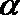
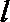
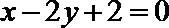
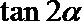
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14.已知函数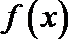
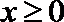
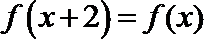
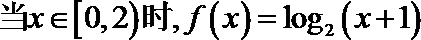
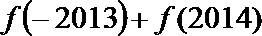
正确答案
-1
解析
解析已在路上飞奔，马上就到！
知识点
15.某校对高三年级的学生进行体检，现将高三男生的体重(单位：kg)数据进行整理后分成六组，并绘制频率分布直方图（如图）．已知图中从左到右第一、第六小组的频率分别为0.16,0.07，第一、第二、第三小组的频率成等比数列，第三、第四、第五、第六小组的频率成等差数列，且第三小组的频数为100，则该校高三年级的男生总数为______.
正确答案
400
解析
解析已在路上飞奔，马上就到！
知识点
16.已知各项均为正数的等比数列
正确答案
解析
解析已在路上飞奔，马上就到！