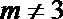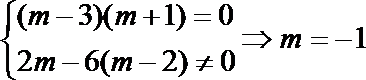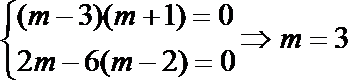数学杨浦区2014年高三试卷

精品

单选题
填空题
简答题

立即下载

数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．若圆C的半径为1，圆心在第一象限，且与直线和轴都相切，则该圆的标准方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

2．已知直线交于A、B两点，O是坐标原点，向量、满足，则实数a的值（）

B－2

C或－

D2或－2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

3．如果点（5，b）在两条平行线6x-8y+1=0，3x-4y+5=0之间，则b应取的整数值为（）

A-4

B4．

C-5

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：单选题

分值: 5分

4．已知A、B两点分别在两条互相垂直的直线和上，且线段的中点为P，则线段AB的长为（）

A11

B10

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

5．若直线与直线互相垂直，则a的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

7．为圆内异于圆心的点，则直线与该圆的位置关系为（）

A相切

B相交

C相离

D相切或相交

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

8．圆心为且与直线相切的圆的方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：单选题

分值: 5分

10．从双曲线的左焦点引圆的切线，切点为，延长交双曲线右支于点P，若M为线段FP的中点，O为坐标原点，则与的大小关系为（）

D不确定

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：单选题

分值: 5分

6．若为圆的弦的中点，则直线的方程（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：单选题

分值: 5分

11．已知两圆x2+y2-10x-10y=0 ，x2+y2+6x+2y-40=0的公共弦长是（）

D10

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

圆的标准方程

题型：单选题

分值: 5分

12．已知点，过点的直线与圆相交于两点，则的最小值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平面向量的概念辨析

题型：单选题

分值: 5分

9．如果点P到点及直线的距离都相等，那么满足条件的点P的个数有（）

A0个

B1个

C2个

D无数个

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

点到直线的距离公式抛物线的定义及应用

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

13．设A（0，3），B（4，5），点P在x轴上，则|PA|+|PB|的最小值是_________，此时P点坐标是____________．

正确答案

，

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

14．设，若直线与轴相交于点A，与y轴相交于B，且与圆相交所得弦的长为2，O为坐标原点，则面积的最小值为___________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

15．与两平行直线：l1：：3x–y+9=0， l2：3x–y–3=0等距离的直线方程为___________．

正确答案

3x–y+3=0

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：填空题

分值: 5分

16．若实数x，y满足的最大值是______________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

19．已知两条直线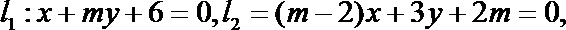求为何值时两条直线：

（1）相交；（2）平行；

（3）重合；（4）垂直．

正确答案

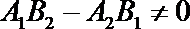
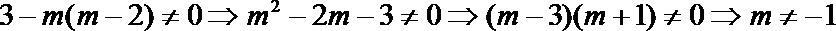
（1）由，得

且

（2）由，

得

（3）由，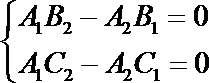

得

（4）由，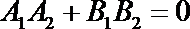

得．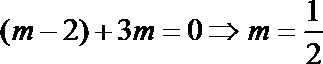

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：简答题

分值: 12分

21．已知点A，点Ｐ是圆上的动点，Ｑ为线段ＡＰ的中点，当点Ｐ在圆上运动时，求动点Ｑ的轨迹方程．

正确答案

设

则

即 …（*）

∵在圆上，

∴ …（**）

将（*）代入（**）得

化简得

动点轨迹方程为：

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：简答题

分值: 10分

17．已知圆，直线。

（Ⅰ）求证：对，直线与圆C总有两个不同交点；

（Ⅱ）设与圆C交与不同两点A、B，求弦AB的中点M的轨迹方程；

（Ⅲ）若定点P（1，1）分弦AB为，求此时直线的方程。

正确答案

（Ⅰ）解法一：圆的圆心为，半径为。

∴圆心C到直线的距离

∴直线与圆C相交，

即直线与圆C总有两个不同交点；

方法二：∵直线过定点，

而点在圆内

∴直线与圆C相交，即直线与圆C总有两个不同交点；

（Ⅱ）当M与P不重合时，连结CM、CP，则，

∴

设，则，

化简得：

当M与P重合时，也满足上式。

故弦AB中点的轨迹方程是。

（Ⅲ）设，

由得，

∴，化简得 ①

又由

消去得（*）

∴ ②

由①②解得，

带入（*）式解得，

∴直线的方程为或。

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：简答题

分值: 12分

18．已知直线，

（1）系数为什么值时，方程表示通过原点的直线；

（2）系数满足什么关系时与坐标轴都相交；

（3）系数满足什么条件时只与x轴相交；

（4）系数满足什么条件时是x轴；

（5）设为直线上一点，

证明：这条直线的方程可以写成．

正确答案

（1）把原点代入，得；

（2）此时斜率存在且不为零

即且；

（3）此时斜率不存在，且不与轴重合，即且；

（4）且

（5）证明：在直线上

。

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

20．已知点到直线：的距离之和为4，求的最小值

正确答案

设与的夹角为，

P到的射影为A，P到的射影为B

，

则

（1）当P位于平面区域I：

时

（2）当P位于平面区域II：

时

的最小值是。

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

22．已知矩形的两条对角线相交于点，边所在直线的方程为：，点在边所在直线上．

（1）求矩形外接圆的方程；

（2）求矩形外接圆中，过点的最短弦所在的直线方程．

正确答案

（1）设点坐标为

且，

又在上，

，，

即点的坐标为。

又点是矩形两条对角线的交点

点即为矩形外接圆的圆心，

其半径

圆方程为

（2）当时，弦BC最短，

，，

所以直线EF的方程为。

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

数学热门试卷