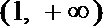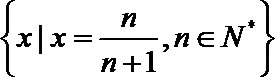数学虹口区2012年高三试卷

精品

填空题
简答题
单选题

立即下载

数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、简答题

3、单选题

真题试卷
模拟试卷

填空题本大题共14小题，每小题4分，共56分。把答案填写在题中横线上。

题型：填空题

分值: 4分

1．函数的定义域是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

题型：填空题

分值: 4分

8．若曲线与直线没有公共点，则的取值范围是_____．

正确答案

－1<b<1

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的定义

题型：填空题

分值: 4分

2．若集合，集合，则（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

补集及其运算

题型：填空题

分值: 4分

7．已知对于任意实数，函数满足。若方程有2013个实数解，则这2013个实数解之和为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

分值: 4分

10．若存在实数满足，则实数a的取值范围是（）

正确答案

a<3

解析

解析已在路上飞奔，马上就到！

知识点

平行关系的综合应用

题型：填空题

分值: 4分

4．方程的解（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：填空题

分值: 4分

6．在△中，已知，三角形面积为12，则（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

9．已知函数，给出下列四个命题：

①为奇函数的充要条件是；

②的图象关于点对称；

③当时，方程的解集一定非空；

④方程的解的个数一定不超过两个。

其中所有正确命题的序号是（）

正确答案

①②③

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

3．化简：（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

5．已知函数是定义在上的偶函数。当时，，则当时，（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

11．若函数的零点都在内，则的最小值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：填空题

分值: 4分

13．已知等差数列（公差不为零）和等差数列，如果关于x的方程

有解，那么以下九个方程，

中，无解的方程最多有（）个

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

点与圆的位置关系

题型：填空题

分值: 4分

14．动点在直角坐标平面上能完成下列动作：先从原点O沿正东偏北方向行走一段时间后，再向正北方向行走，但何时改变方向不定。假定速度为10米/分钟，则行走2分钟时的可能落点区域的面积是（）

正确答案

100-200

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：填空题

分值: 4分

12．设集合，如果满足：对任意，都存在，使得，那么称为集合A的一个聚点，则在下列集合中：

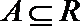
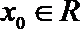
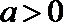
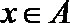
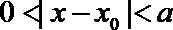
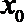
①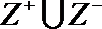

②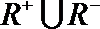

③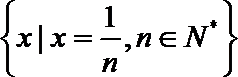

④

以0为聚点的集合有（）（写出所有你认为正确结论的序号）

正确答案

②，③

解析

解析已在路上飞奔，马上就到！

知识点

补集及其运算

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 14分

21．若函数，如果存在给定的实数对，使得恒成立，则称为“函数”

（1）判断下列函数，是否为“函数”，并说明理由；① ②

（2）已知函数是一个“函数”，求出所有的有序实数对。

正确答案

（1）解：①若是“函数”

则存在实数对，使得

即时，对恒成立

而最多有两个解，矛盾

因此不是“函数”

②对一切都成立，存在实数对

使得

即存在常数对满足，

故是“函数”

（2）解：函数是一个“函数”

设有序实数对满足，

则恒成立

当时，

，不是常数；

因此，

当时，

则有，

即恒成立，

所以

当时，

满足是一个“函数”的实数对

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：简答题

分值: 12分

19．已知，求的值

正确答案

原式

又

解析

解析已在路上飞奔，马上就到！

知识点

诱导公式的作用

题型：简答题

分值: 14分

20．已知函数

（1）求证：函数在内单调递增；

（2）记为函数的反函数。若关于的方程在上有解，求的取值范围。

正确答案

证明：（1）任取，

则

，

即函数在内单调递增.

（2），

解法一：，

当时，，

的取值范围是.

解法二：解方程，

得，，

解得 .

的取值范围是

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 18分

23．设函数，其中为正整数．

（1）判断函数的单调性，并就的情形证明你的结论；

（2）证明：；

（3）对于任意给定的正整数，求函数的最大值和最小值．

正确答案

（1）在上均为单调递增的函数. 对于函数，

设，则，，函数在上单调递增

（2）原式左边

又原式右边.

（3）当时，函数在上单调递增，的最大值为，

最小值为. 当时，，函数的最大、最小值均为1.

当时，函数在上为单调递增. 的最大值为，

最小值为.当时，函数在上单调递减，

的最大值为，最小值为. 下面讨论正整数的情形：

当为奇数时，对任意

且，

以及，

，从而 . 在上为单调递增，则的最大值为，

最小值为. 当为偶数时，

一方面有 .另一方面，由于对任意正整数. 函数的最大值为，

最小值为. 综上所述，当为奇数时，函数的最大值为，最小值为. 当为偶数时，函数的最大值为，最小值为

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 16分

22．设m为实数，函数，

（1）若≥4，求m的取值范围；

（2）当m＞0时，求证在上是单调递增函数；

（3）若对于一切，不等式恒成立，求实数m的取值范围。

正确答案

（1）

当时，，无解；

当时，，

解得. 所以.

（2）由于.

所以.

任取，

所以

即：在为单调递增函数.

解二：由（2）结论得：

是单调递增函数，

所以只要，

得，

当时不等式显然成立；

当时，解得：，

综上得：．

解析

解析已在路上飞奔，马上就到！

知识点

指数函数单调性的应用

单选题本大题共4小题，每小题5分，共20分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

17．已知函数的图像关于点P对称，则点P的坐标是（）

D（0，0）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线和圆的方程的应用

题型：单选题

分值: 5分

15．已知函数若，则的取值范围是（）

B或

D或

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

18．若直角坐标平面内的两点P．Q满足条件：

①P．Q都在函数的图像上；②P．Q关于原点对称，则称点对（P，Q）是函数的一个“友好点对”（点对（P，Q）与（Q，P）看作同一个“友好点对”）．

已知函数则此函数的“友好点对”有（）对．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：单选题

分值: 5分

16．函数的反函数图像是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

数学热门试卷