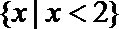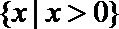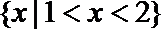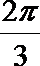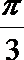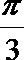1.设集合A={x|0<x<2},集合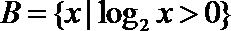
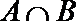
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 如果一个几何体的三视图如图所示(长度单位: cm), 则此几何体的表面积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知函数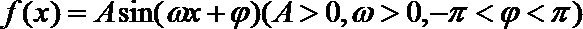
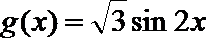

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 下列四个结论:
①若

②命题“若

③“命题

④命题“

其中正确结论的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 某程序框图如下图所示,该程序运行后输出的
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.显示屏有一排7个小孔,每个小孔可显示0或1,若每次显示其中3个孔,但相邻两孔不能同时显示,则该显示屏能显示信号的种数共有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在复平面内,复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
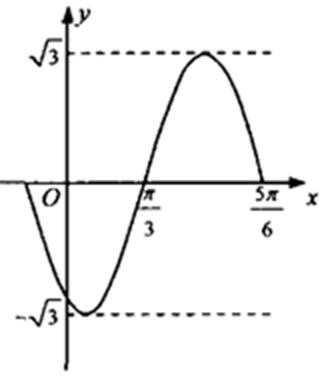
10.函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图. 其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第6幅图的蜂巢总数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.过曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 如图,矩形ABCD的四个顶点的坐标分别为A(0,—1),B(



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 实数





正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
14.正四棱锥


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 设f(x)与g(x)是定义在同一区间D上的两个函数,若

①f(x)=x2+1与g(x)=x2+
②f(x)=x2﹣3x+4与g(x)=2x﹣3的一个“远离区间”可以是[2,3];
③f(x)=



④若f(x)=

其中的真命题有_________.(写出所有真命题的序号)
正确答案
①③
解析
解析已在路上飞奔,马上就到!
知识点
13. 在二项式

正确答案
-56
解析
解析已在路上飞奔,马上就到!
知识点
请从22~24三题中任选一题作答。
22.选修4—1:几何证明选讲
如图所示,圆O的直径为BD,过圆上一点A作圆O的切线AE,过点D作DE⊥AE于点E,延长ED与圆O交于点C.
(1)证明:DA平分∠BDE;
(2)若AB=4,AE=2,求CD的长.
23.选修4—4:坐标系与参数方程
已知曲线





(1)化

(2)若








24.选修4—5: 不等式选讲
(1)解不等式
(2)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 请从【1】【2】两题中任选一题作答。
【1】已知


(1)求
(2)若

【2】已知数列








(1)求数列

(2)记



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 己知函数
(1)若 

(2)若关于x的不等式 
(3)若 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆



(1)求椭圆
(2)如图,以椭圆











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸.呼吸困难等心肺疾病。为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了列联表:已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为
(1)将上面的列联表补充完整;
(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明理由;
(3)已知在患心肺疾病的10位女性中,有3位又患胃病.现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 如图,在四棱锥







(1)求证:
(2)已知二面角





正确答案
解析
解析已在路上飞奔,马上就到!