1．函数f（x）=2x-1的反函数f -1（x）=_____________
正确答案
log2（x+1），x∈（-1，+∞）
解析
解析已在路上飞奔，马上就到！
知识点
2．设集合
正确答案
（-1，2）
解析
解析已在路上飞奔，马上就到！
知识点
4．△ABC的面积为3，AB=2，AC=5，则cosA=______________．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．若|sinx|＜cosx，则x的取值范围是___________．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．若正数x，y满足x+3y=5xy，则3x+4y的最小值是______________．
正确答案
5
解析
解析已在路上飞奔，马上就到！
知识点
10．函数f（x）=asinωx+bcosωx的图象如图所示，则（a，b）=________
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．公比为
正确答案
5
解析
解析已在路上飞奔，马上就到！
知识点
5．设f（x）=|lgx|，若a≠b，且f（a）=f（b），则a·b=______________．
正确答案
1
解析
解析已在路上飞奔，马上就到！
知识点
6．函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．无穷数列{an}前n项和
正确答案
-1
解析
解析已在路上飞奔，马上就到！
知识点
14．设数列{an}中，相邻两项an，an+1是方程x2-nx+bn=0的两根，且a10=7，则b17=_____
正确答案
66
解析
解析已在路上飞奔，马上就到！
知识点
11．已知函数f（x）=loga（2-ax）在区间[0，1]上单调递减，则a的取值范围是______________．
正确答案
（1，2）
解析
解析已在路上飞奔，马上就到！
知识点
12．数列{an}的通项公式
正确答案
3018
解析
解析已在路上飞奔，马上就到！
知识点
13．已知
正确答案
5
解析
解析已在路上飞奔，马上就到！
知识点
15．设{an}是等比数列，则“a1<a2<a3”是“数列{an}是递增数列”的 （ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．f（x）是R上以2为周期的奇函数，当x∈（0，1）时，
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．设函数y=f（x）的反函数f -1（x）存在，将y=f（x）的图象向左平移1个单位得到图象C1，再将C1向上平移1个单位得到图象C2，作出C2关于直线y=x对称的图象C3，则C3的解析式为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．对任意的实数α、β下列等式恒成立的是（ ）
A2sinαcosβ=sin（α+β）+sin（α-β）
B2cosαsinβ=sin（α+β）+cos（α-β）
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．在△ABC中，角A、B、C的对应边分别为a、b、c，若lga-lgb=lgcosB-lgcosA。
（1） 判断△ABC的形状；
（2） 若a、b满足：函数y=ax+3的图象与函数
正确答案
（1） 由lg
于是sin2A=sin2B，
所以三角形ABC为等腰三角形或直角三角形；
（2） 因为y=ax+3的反函数
所以a=3，b=1，
从而
解析
解析已在路上飞奔，马上就到！
知识点
20．已知数列{an}中，a1=2，a2=3，其前n项和Sn满足Sn+1+Sn-1=2Sn+1（n≥2，n∈N*）．
（1） 求数列{an}的通项公式；
（2） 设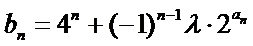
正确答案
（1） 由已知，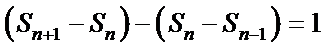
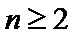
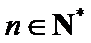
即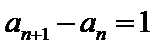
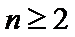
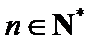
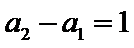
∴数列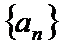
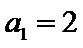
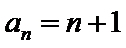
（2） ∵
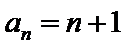
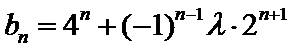
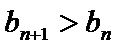
即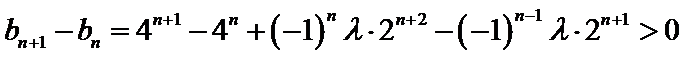
∴
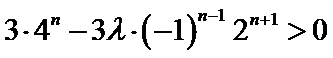
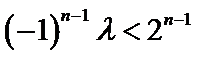
1°当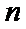
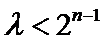
∵当且仅当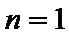
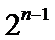
2°当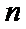
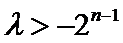
∵当且仅当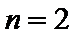
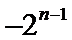
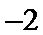
故-2<λ<1，又λ为非零整数，则λ=-1．
综上所述，存在λ=-1，使得对任意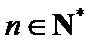
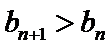
解析
解析已在路上飞奔，马上就到！
知识点
22．某学校要建造一个面积为10000平方米的运动场．如图，运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成．跑道是一条宽8米的塑胶跑道，运动场除跑道外，其他地方均铺设草皮．已知塑胶跑道每平方米造价为150元，草皮每平方米造价为30元．
（1） 设半圆的半径OA=r （米），试建立塑胶跑道面积S与r的函数关系S（r）；
（2） 由于条件限制r∈[30，40]，问当r取何值时，运动场造价最低?（精确到元）
正确答案
（1） 塑胶跑道面积
（2） 设运动场造价为y，
则 
∵r∈[30，40]，函数y是r的减函数，
∴当r=40时，运动场造价最低为636510元
解析
解析已在路上飞奔，马上就到！
知识点
21．已知函数
（1） 求m、n的值；
（2） 若将函数y=f（x），x∈R的图象按向量
正确答案
（1） 
1°若
解得
2°若m<0，则可解得
（2） 令
1°当m=3，n=-2时，
2°当m=-3，n=1时，
解析
解析已在路上飞奔，马上就到！
知识点
23．设数列{an}的通项公式为an=pn+q（n∈N*，p>0）．数列{bn}定义如下：对于正整数m，bm是使得不等式an≥m成立的所有n中的最小值．
（1） 若
（2） 若p=2，q=-1，求数列{bm}的前2m项和公式；
（3） 是否存在p和q，使得bm=3m+2（m∈N*）？如果存在，求p和q的取值范围；如果不存在，请说明理由．
正确答案
（1） 由题意，得
∴
（2） 由题意，得an=2n-1，对于正整数，由anm，得
根据bm的定义可知，当m=2k-1时，bm=k（k∈N*）；当m=2k时，bm=k+1（k∈N*）；
∴b1+b2+···+b2m=（b1+b3+···+b2m-1）+（b2+b4+···+b2m）=（1+2+3+···+m）+[2+3+4+···+（m+1）]
（3） 假设存在p和q满足条件，由不等式pn+qm及p>0，得
∵bm=3m+2（m∈N*），根据bm的定义可知，
对于任意的正整数m都有
即-2p-q（3p-1）m<-p-q对任意的正整数m都成立，
当3p-1>0（或3p-1<0）时，可得
当3p-1=0，即
∴存在p和q，使得bm=3m+2（m∈N*）．
p和q的取值范围分别是
解析
解析已在路上飞奔，马上就到！