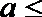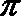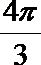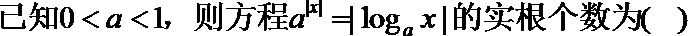1.命题“若


正确答案
若a≠0且b≠0,则ab≠0
解析
解析已在路上飞奔,马上就到!
知识点
3.要使
正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
6.用数学归纳法证明“


正确答案
2(2k+1)
解析
解析已在路上飞奔,马上就到!
知识点
8.已知






正确答案

解析
解析已在路上飞奔,马上就到!
知识点
2.已知点M(a,b)与N关于


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知不等式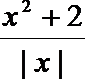
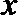
正确答案
a≤2
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.如图,在矩形







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设











以上结论正确的是_________________(写出所有正确结论的编号).
正确答案
(2)(3)(4)
解析
解析已在路上飞奔,马上就到!
知识点
14.设数列








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数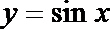
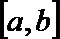
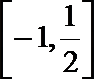
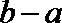
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知




条件




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.实数
(1)与复数
(2)对应的点在
正确答案
(1)根据共轭复数的定义得
解之得m=1.
(2)根据复数z对应点在x轴上方可得m2-2m-15>0,
解之得m<-3或m>5.
解析
解析已在路上飞奔,马上就到!
知识点
20. 若向量

(1)求



(2)设△







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知等差数列


(1)若




(2)若




正确答案
(1)设等差数列



由题意得

所以由等差数列通项公式可得


故

当






当






故
记数列


综上,


解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数


(1)求
(2)当






(3)若在函数定义域内总存在区间




正确答案
(1)由已知可得,
且函数的定义域为D=
又
于是,b=0(
又对任意
综上,
解析
解析已在路上飞奔,马上就到!
知识点
23.将数列
记表中的第一列数






(1)求
(2)证明数列{

(3)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当



正确答案
(1)
(2)证明:由已知
(3)解:设上表中从第三行起,每行的公比都为q,且q>0.
因为
所以表中第1行至第12行共含有数列{an}的前78项,
故 a81在表中第13行第三列,
因此
又
所以 q=2.
记表中第k(k≥3)行所有项的和为

解析
解析已在路上飞奔,马上就到!