1.集合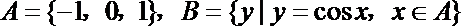
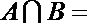
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知a > 0,b > 0,a、b的等差中项是

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知函数

① 函数
②函数
③

④

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在等比数列
正确答案
240
解析
解析已在路上飞奔,马上就到!
知识点
11.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 函数




①函数
②当
③函数
④函数
其中正确命题序号是_______________.
正确答案
①②③④
解析
解析已在路上飞奔,马上就到!
知识点
14.设a > 1,函数
(1)求

(2) 若
(3)若
正确答案
解:
(1) 由
∴
∴
(2) ∵ a > 1 ∴ 
∴ 
∴ 
∴
(3)
要使
只需
∴
∴
因此,a的取值范围为
解析
解析已在路上飞奔,马上就到!
知识点
13.设函数

(1)求b、c的值;
(2)求
正确答案
(1) ∵
∴
∵ 

即
∴ 
(2) ∵
∴
由
由
∴ 

解析
解析已在飞奔的路上,马上就到!








































