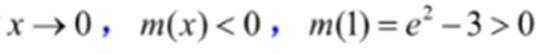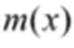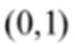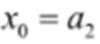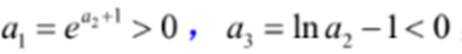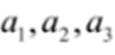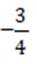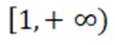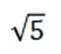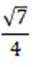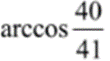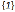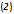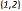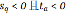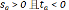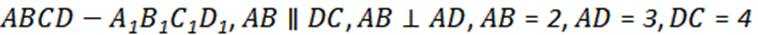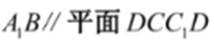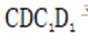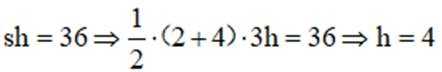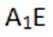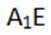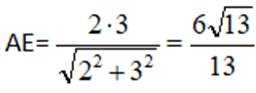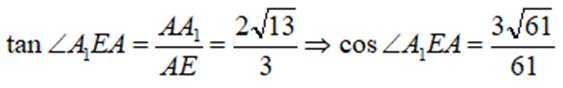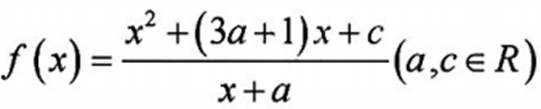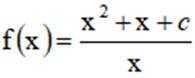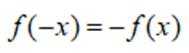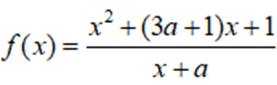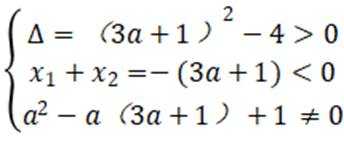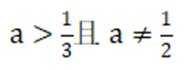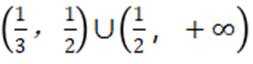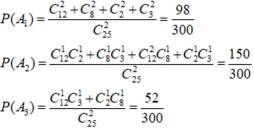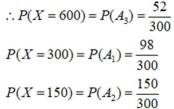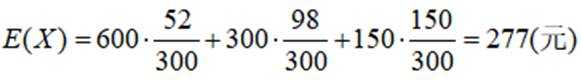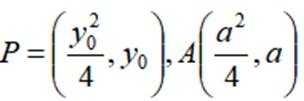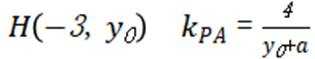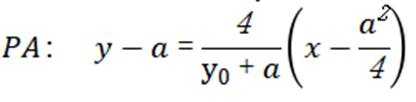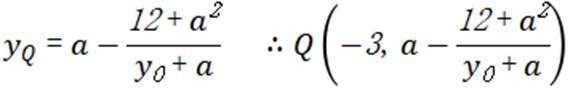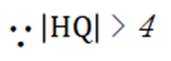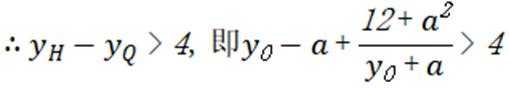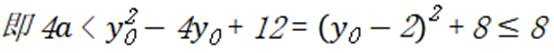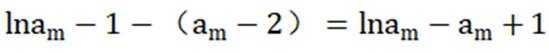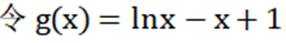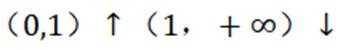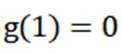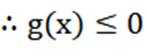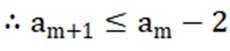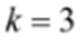不等式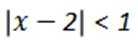
正确答案
(1,3)
已知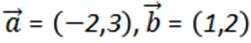
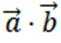
正确答案
4
3.已知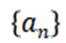
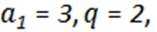
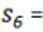
正确答案
189
4.已知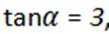
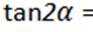
正确答案
5.已知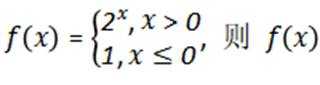
正确答案
已知当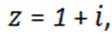
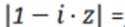
正确答案
7.已知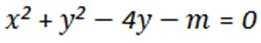
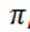
正确答案
-3
8.在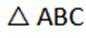
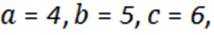
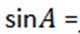
正确答案
9.国内生产总值(GDP)是衡量地区经济状况的最佳指标,根据统计数据显示,某市在2020年间经济高质量增长,GDP稳步增长,第一季度和第四季度的GDP分别为231和242,且四个季度GDP的中位数与平均数相等,则2020年GDP总額为 ;
正确答案
946
10.已知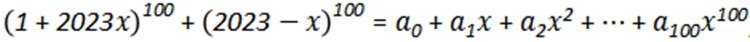
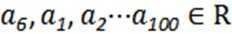
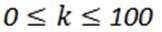
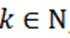
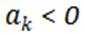
正确答案
49
公园修建斜坡,假设斜坡起点在水平面上,斜坡与水平面的夹角为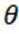
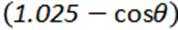
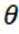
正确答案
12.空间内存在三点A、B、C,满足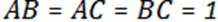
正确答案
9
13.已知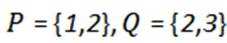
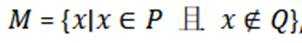
正确答案
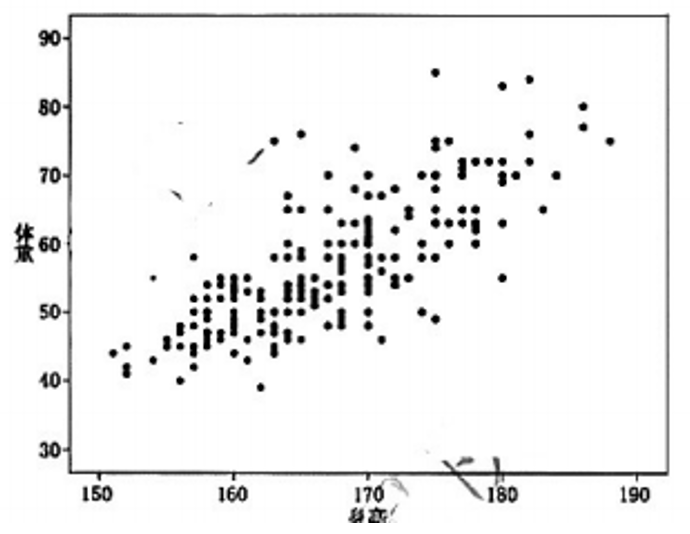
根据身高和体重散点图, 下列说法正确的是()
正确答案
15.设
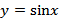
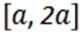
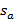
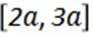
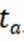
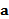
正确答案
16.在平面上,若曲线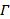
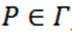
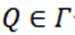
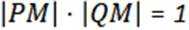
(1)所有椭圆都是“自相关曲线"
(2)存在是“自相关曲线”的双曲线
正确答案
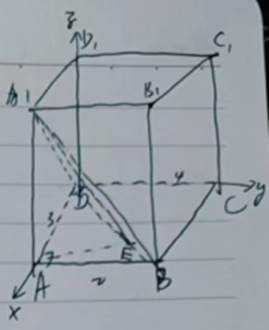
17.直四棱柱
(1)求证:
(2)若四棱柱体积为36,求二面角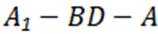
正确答案
(1)因为AB平行于CD,所以AB与平面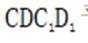
又因为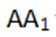
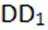
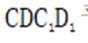
因为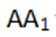
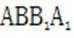
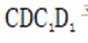
因为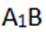
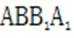
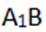
(2)因为四棱柱体积为36,设AA1=h
所以
在底面内作AE垂直BD与E,连
因为BD垂直AE,BD垂直于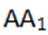
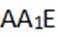
所以
在直角三角形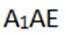
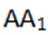
所以
18.函数
(1)当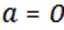
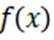
(2)函数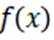
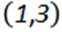
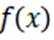
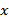
正确答案
(1)当a=0时,
定义域为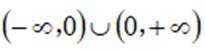
假设
所以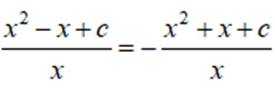
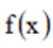
所以不存在实数c,使得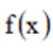
(2)因为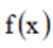
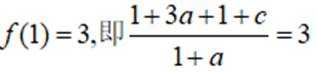
所以
令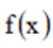
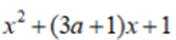
因为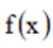
所以
所以
所以a的取值范围为
21世纪汽车博览会在上海2023年6月7日在上海举行,下表为某汽车模型公司共有25个汽车模型,其外观和内饰的颜色分布如下表所示:
(1)若小明从这些模型中随机拿一个模型,记事件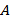
求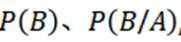
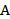
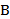
(2)该公司举行了一个抽奖活动,规定在一次抽奖中,每人可以一次性从这些模型中拿两个汽车模型,给出以下假设:


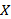
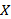
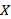
正确答案
(1)
(2)设三种结果:内外均同,内同或外同,内外均不同分别为事件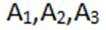
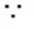
分布列
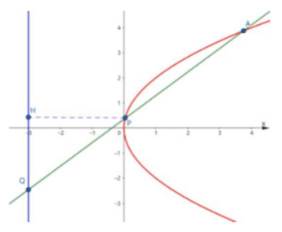
曲线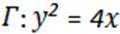
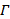
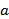
(1)若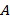
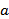
(2)若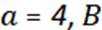
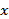
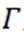
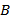
(3)直线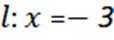
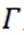

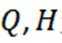
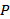
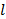
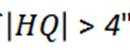
正确答案
(1)由题意得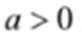
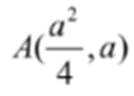
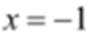
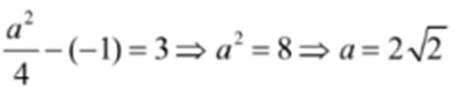
当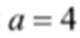
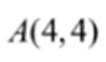
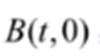
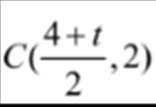
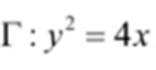
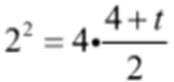

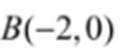
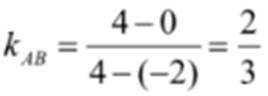
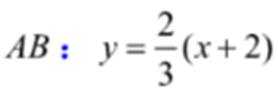
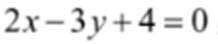
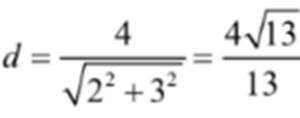
(3)设
由已知:
令x=-3,
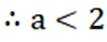
令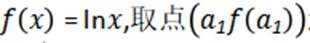
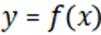
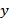
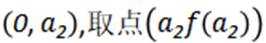

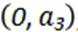
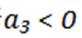
(1)若正整数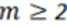
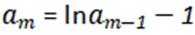
(2)若正整数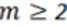
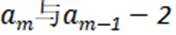
(3)若正整数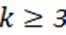
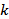
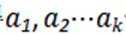
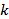
正确答案
(1)由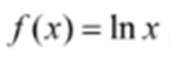
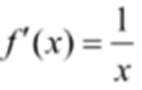
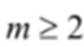
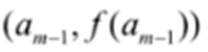
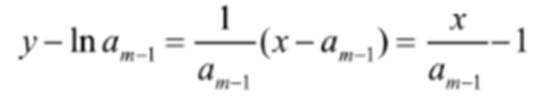
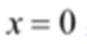
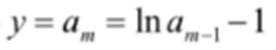
(2)
即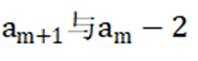
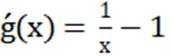
X=1时
(3)假设存在k,使得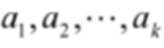
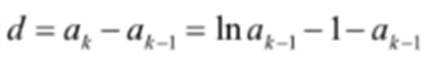

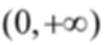
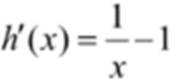
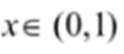
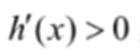
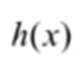
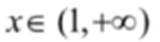
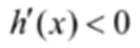
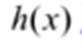
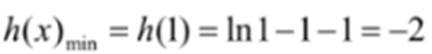
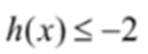

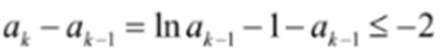
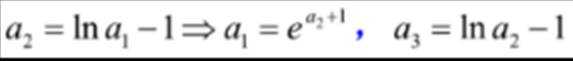
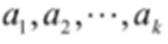
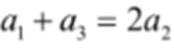
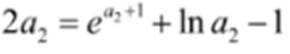
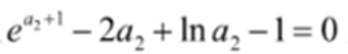
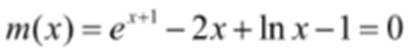
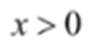
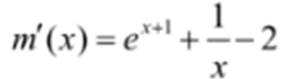

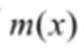
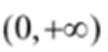
结合数列的单调性,因为